AUCTORES
Globalize your Research
Review Article
*Corresponding Author: Jean-Louis Bretonnet, Université de Lorraine 1 Bd. François Arago, Metz F-57078, France
Citation: Jean-Louis Bretonnet (2019) Interactions in atomic and ionic liquids. J. International Journal of Materials Science and Engineering, 1(1); DOI: 10.31579/2637-8914/003
Copyright: © This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.
Received: 07 October 2019 | Accepted: 02 December 2019 | Published: 10 December 2019
Keywords: -
This review seeks to describe, from first principles, the nature of the interaction forces in atomic and ionic liquids. The atoms and molecules made up of dipoles and multipoles interact with van der Waals forces, while the ionic systems are viewed as pseudoions interacting through effective forces depending on the electronic structure and the physical ionic arrangement. The interplay between these two aspects of materials is quite complex and forms the main subject of this review.
As it will be shown, the two-component system of interacting electrons and ions can be reduced, in second order perturbation theory, to an effective one-component system made up of pseudoions acting under the influence of two-body, central, screened potentials. These potentials result from a weak interaction between the electrons and the ions, deduced from the pseudopotential theory.
Once the interatomic forces are known, the atomic structure and the electronic transport properties can be determined by methods of classical mechanics and quantum mechanics. Besides, a large volume-dependent term in the free energy, independent of the ionic positions, which distinguishes the conducting liquids from the simple isolator liquids like argon, is indispensable for explaining the thermodynamically properties.
A liquid is a phase of condensed matter in which the density is further removed from that of the gas phase than that of the corresponding solid phase. Because of this large difference of density between liquids and gases, the thermodynamic functions of liquids cannot be developed as a function of the density, as done for the gases. But, although the density of liquids is close to that of solids, at a similar temperature, the lack of translational symmetry and long-range order doesnot allow a theoretical description of liquids as easily as for solids.
Liquids have been classified for a long time according to their electronic or atomic transport properties. For example, the liquids (like solids) can be divided into insulators and conductors; for conductors, it must be still indicated whether the conduction is ionic (the conductivity of molten salts varies from 1 to 103 Ω−1.m−1) or electronic (the conductivity of liquid metals is of the order of 106 Ω−1.m−1). However, the liquids can also be classified according to their ability to flow more or less easily. While most of simple liquids have low dynamic viscosities (10−3 Pa.s), certain organic fluids may have viscosities much larger (1 Pa.s).
Among the possible classifications of liquids, the least controversial is the one made on the basis of the interactions acting between atoms or molecules, because a specific interaction dominates in each type of liquid. This review is solely devoted to the simple liquids that is to say to liquids characterized by interactions in spherical symmetry whose forces have the center of mass of the particles as the application point. For such systems, the potential energy U is written as a sum of N-body potentials:
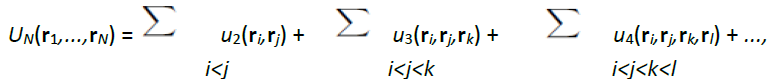
where u2(ri,rj) is the 2-body potential, u3(ri,rj,rk) the 3-body potential, etc. This notation clearly indicates that if three particles (i,j,k) are interacting, their potential energy consists of the sum of the 2-body potential [u2(ri,rj) + u2(rj,rk) + u2(rk,ri)] plus the 3-body potential u3(ri,rj,rk).
The most representative simple liquids are the noble gases: argon, krypton, xenon as classic liquids, as well as neon and helium, which are considered as quantum liquids when the de Broglie wavelength of the atoms is of the same order of magnitude as the interatomic distance. At low densities, the methane (CH4) can also be regarded as a simple liquid because it consists of nearly spherical molecules.
In the category of simple liquids, enter also, without restriction, the liquid metals such as alkali metals (Na, K, Cs ...), noble metals (Ag, Au, Cu) and most of polyvalent metals. Germanium and silicon can also be seen as such, although they have a pronounced tendency to form covalent bonds. Unlike the noble gas atoms, the metal atoms have incomplete electron shells occupied by the valence electrons forming a gas of nearly free electrons. Thus, it may seem strange that a metal, composed of ions immersed in an electron gas, can be regarded as a simple liquid. In fact, this is legitimate to the extent that the metal can be thought of as a set of pseudoions interacting with a pseudopotential, the concept of which was developed by Phillips and Kleinman[1]. Although the concept of pseudopotential is more difficult to justify for the transition metals and rare earth metals than for the normal metals (alkali and polyvalent) - due to the hybridization effects between the valence electrons and core electrons - the fact remains that, from a structural point of view, all the liquid metals are considered as simple liquids. It should be mentioned that the pseudopotential formalism is a powerful tool used to define the pair potential in liquid metals, which depends on the density and temperature, unlike the pair potential of the rare gases.
Binary alloys and liquids having important directional effects will not be investigated here. Examples of these liquids are the homonuclear (N2, O2 , H2) and heteronuclear (CO) molecular liquids, the associated liquids (water, glycerol ...) characterized by hydrogen bonds and the polar liquids (HBr, SO2...) whose molecules have a strong asymmetry or pronounced electrostatic interactions.
Another class of simple liquids, with a structural length scale between 10 nanometers and one micron (1000 nm), will not be investigated either. These systems are composed of mesoscopic particles 1000 times larger than atoms, immersed in an aqueous solution. They include the colloidal suspensions, spherical polymers, biological macromolecules, etc. Although they are more sensitive to mechanical stresses than the atomic systems, their thermodynamic and structural properties can be calculated with the same theoretical models as those of the atomic systems. Their interparticle potentials will be examined in another paper.
Typology of Microscopic Interactions
2.1 Interactions at Short and Long Distances
The low compressibility and the relatively high density of liquids show respectively the existence of repulsive forces at short distances and attractive forces at long distances. The repulsive forces prevent the collapse of the matter on itself and the attractive forces give the cohesive properties. Generally the interactions between two entities (molecules or atoms are investigated in terms of
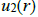
and not in terms of force

The potential energy (potential) is calculated using quantum mechanics.
The potential associated with the repulsive forces between two atoms not overlapping, has usually the form:
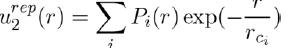
Where Pi(r) are polynomials in r and rci parameters depending on the individual atoms. This interaction potential takes into account the electrostatic repulsion exerted between the two nuclei and the effects due to the Pauli Exclusion Principle. In practice, simplified forms of
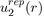
are used such as that of Born and Mayer [2]:
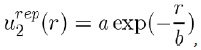
(1)
Where a and b are two constants determined by adjusting certain physical properties of the experimental results. But the value of b can also be estimated with good accuracy by the relation
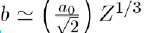
where a0 (= 0,0529 nm) is the Bohr radius and Z the atomic number.Sometimes the following formula, in inverse power of r, is used:
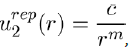
(2)
Where c and m are two constants to be determined
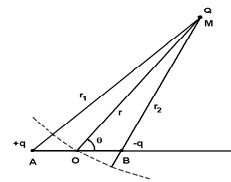
Figure 1: Schematic representation of the dipole AB interacting with the point charge Q.
Regarding the potentials associated with the attractive forces at long range, they contain various contributions that are better known than those of the repulsive potential. These attractive forces, discovered by London but called the van der Waals forces, result from the presence of dipoles or multipoles in molecules and atoms.
Interaction between a Dipole and a Point Charge
In this subsection we recall the calculation of the potential energy of interaction between a dipole and a point charge (monopole), which is at the basis of the study of the van der Waals forces. An electrostatic dipole consists of a pair of two point charges of opposite signs, +q and −q, located at points A and B. The electric dipole moment is defined by the vector p:

(3)
To calculate the potential energy of interaction between the dipole and a point charge Q, we fix the point O in the middle of AB = l and assume that the charge Q is located at the distance OM = r (with r ≫ l) in the direction θ (Fig. 1). The potential energy is given by Coulomb’s law:

(4)
Where: so that:
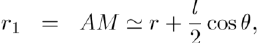
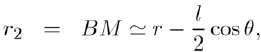

(5)
substituting this result in equation (4), and taking into account of equation (3), we are in position to write the potential energy u(r) in the form:
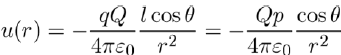
(6)
It should be noted, in passing, that the electric field created by the dipole at the point M is E = −gradV, where V is the electrostatic potential associated with the potential energy u(r) by the relation u(r) = Q.V (r). Therefore, the electric field modulus at the point M is expressed as:
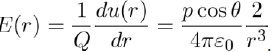
(7)
Intermolecular Interactions
Often, the potential energy is calculated between a set of charges qi, gathered in a small volume, and a point charge Q located at a distance r of this volume.
If the sum of charges in the volume is not zero (qi = 0, as in an ion), it can be taken that the total charge


is concentrated at the centroid, so that the potential energy is calculated with the formula:

But to get better accuracy, the calculation has to be performed for all the individual charges, which amounts to evaluating the potential energy u(r) as an expansion in powers of 1/r.
If the sum of charges in the volume is zero (

qi = 0, as in a molecule), the first term of the series in 1/r is zero. In addition, if all the charges qi are reduced to a dipole (consisting of one charge −q and one charge +q), the potential energy between the point charge Q and this dipole is given by equation (6). It is proportional to 1/r2. But it may happen that the charges are reduced, not to a dipole, but to a quadrupole (set of 4 charges

arranged symmetrically about the centroid). In this case, the term 1/r2 is zero and the potential energy between the point charge Q and the quadrupole is proportional to 1/r3. If there is no quadrupole, the term 1/r3 is nonexistent and an octupole (set of 8 charges arranged symmetrically around the centroid) must be considered, and so on. Thus, a set of charges can be decomposed into multipoles (dipoles, quadrupoles, octupoles...) playing a significant role in certain circumstances.
The simplest polar systems are formed of monopoles. These systems, such as molten salts, consist of charges Q = ze (e.g. NaCl composed of charges +e and −e). Other polar systems are made up of permanent dipoles (hydrogen bromide composed of uncharged molecules with a dipole moment pd) or still of permanent quadrupoles (liquid nitrogen composed of molecules having a quadrupole moment pq). The potential energies between these various entities are calculated by direct application of the laws of electrostatics. For example, the potential energy between one point charge Q and one dipole moment pd is given by equation (6), i.e.:

Similarly, the potential energy between one point charge Q and one quadrupole moment pq is calculated with the formula:
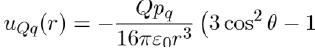
In the case of the potential energy between two dipoles of dipole moments pd1 and pd2, it is expressed as:
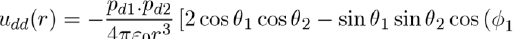
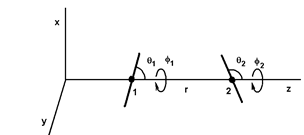
Figure 2: Positions and orientations of two dipoles separated by r along the z axis. The orientations are defined by the angles θ1, φ1, θ2 and φ2.
Thus, it is possible to calculate the potential energies between all the entities: monopolemonopole (QQ), monopole-dipole (Qd), monopole-quadrupole (Qq), monopole-octupole (Qo)..., dipole-dipole (dd), dipole-quadrupole (dq)..., quadrupole-quadrupole (qq) ... and so on. All these expressions are given for specific position and orientation of the entities. As an example, figure (2) shows two dipoles separated by r on the z axis, where θ1 and θ2 are the angles between the dipoles and the z axis, and φ1 and φ2 are the azimuth angles. The five parameters r, θ1, θ2, φ1 and φ2 completely determine the positions of the two dipoles and the potential energy udd(r, θ1, θ2, φ1, φ2).
Keesom[3] suggested calculate the thermodynamic properties of these systems with the average potential energy u(r,T), obtained by integrating u(r) over all orientations of the molecules according to the relation:
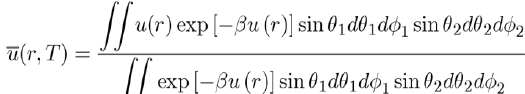
(8)
Where the Boltzmann factor exp (−βu) is used, with

in order to give a greater weight to the orientations of molecules corresponding to states of lowest energy. As a result, the average potential energy
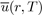
loses its angular dependence, but acquires a temperature dependence. Since these integrals are very difficult to calculate, the Taylor expansion of the exponential function is generally used around the average value of the potential energy, i.e.:
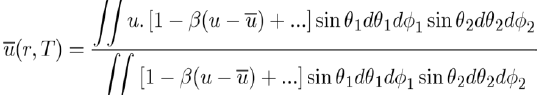
This expression allows the evaluation of

by the equation [4]:
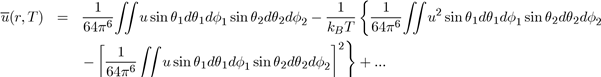
Below the expressions are shown for the average potential energies of the main molecular entities (monopole-monopole QQ, monopole-dipole Qd, monopole-quadrupole Qq and dipole-Dipole dd:
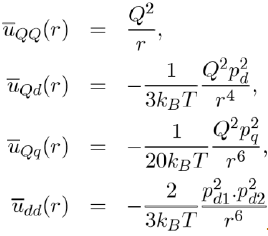
(9)
It is found that the greater the number of poles in a molecule, the faster the potential energy drops away with distance. Thus, the potential energy between monopoles varies like r−1, the dipole-monopole potential energy like r−4, the dipole-dipole potential energy like r−6. It is also demonstrated that the dipole-quadrupole potential energy varies like r−8, the quadrupolequadrupole potential energy like r−10, etc.
Sometimes a set of charges having no permanent dipole moment acquires an electric dipole moment when placed in an electric field. Indeed, it can be understood that a molecule composed of electrons and nuclei with no permanent dipole moment can, under the action of an external electric field, see the electrons and nuclei move in opposite directions, creating a new equilibrium configuration with an induced dipole moment. Naturally, superimposing permanent dipole moments on induced dipole moments is possible. In this case, the potential energy is composed of two contributions. One is due to the interaction between permanent dipoles and the other to the interaction between induced dipoles.
Usually, the purely electrostatic forces between polar molecules (permanent dipoles) are weaker than those acting between nonpolar molecules (induced dipoles), and might be therefore neglected. By contrast, in highly polar molecules, such as those of water or acetone, the electrostatic forces are masked by strong chemical interactions that depend on the orientation. These will not be discussed here.
Interatomic Interactions
The electrostatic forces, which have been described in the case of spherical molecules (nonpolar), gain a special importance in the case of atoms. The reason is that the fluctuations of electron density in an atom produces an instantaneous dipole. Indeed, the movement of the electrons around the nucleus moves the centroid of negative charges, and contributes to the formation of an instantaneous dipole that fluctuates in magnitude and direction at the rotation frequency of the electrons (∼ 1015 s−1). In addition, the electric field created by the instantaneous dipole affects the movement of electrons in a neighboring atom giving rise to an induced dipole, which fluctuates in phase with the first dipole. Generally, the two dipoles are aligned and exert one upon another a force of attraction. This force is called the dispersion force for the following reason. The electric field created by the instantaneous dipole of the first atom propagates at the speed of light towards the second atom, and the dipole induced in the second atom in turn emits an electric field in direction to the first atom. If the two atoms are close enough, the two dipoles fluctuate in phase and their directions are identical. But if the atoms are far apart from each other, a phase shift occurs between the electric fields, hence a disorientation of the dipoles

And a decrease in the strength of interaction. This effect is comparable to the dispersion of light in a medium of given refractive index.
The calculation of dispersion forces was made by London [5] with the perturbation theory of quantum mechanics, but the general expression can be established simply [6] using the model of the Bohr atom1. Considering the Bohr atom, it can be assumed that the instantaneous dipole moment, created between the nucleus and the electron, is roughly speaking (Eq. 3):

(10)
Where e is the electron charge and a0 the Bohr radius:
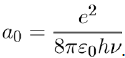
(11)
The energy of the Bohr atom in its ground state, also called the ionization potential, is I = hν, where ν (= 3, 3.1015 s−1) is the characteristic frequency associated with the movement of the electron in its orbit.
The electric field produced by an instantaneous dipole at distance r from the atom (Eq. 7) is on average:
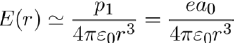
(12)
The energy of the Bohr atom in the ground state is: \

With:

But E0 (= −hν) also corresponds to the energy of the electron on its lowest orbit, of radius:
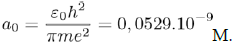
Then, the characteristic frequency associated with the movement of the electron on its orbit is given by the expression:

Which links a0 with ν.
However, a second neutral atom situated in this electric field, at distance r, undergoes a polarization and acquires an induced dipole moment:

(13)
Where α is the polarizability of this atom. This quantity, which measures the ability to move the electronic distribution in the atom, is proportional to the volume of the atom:

(14)
Thus the potential energy of attraction between the dipoles p1 and p2 is obtained by performing the product of the dipole moment of the second atom (Eq. 13) by the electric field, on this spot, created by the first atom (Eq. 12), namely:

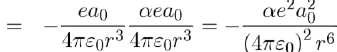
Therefore, using equations (11) and (14), the potential energy between two atoms separated by distance r is written as:
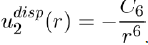
(15)
Where the constant
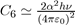
depends on the square of the polarizability α and the ionization potential hν, as could be demonstrated by a precise calculation using quantum mechanics In dense systems, the presence of a third atom brings a further contribution to the twobody potential (Eq. 15). This is a three-body potential calculated by taking into account the dispersion forces between three dipoles [7], [8]. The analytical expression of the triple dipole potential, varying as r−9, is expressed as a function of the atomic polarizability α and the constant C6 as:
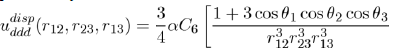
(16)
Where the angles θ1, θ2 and θ3 are those of the triangle formed by three atoms (1,2,3) with sides r12 = |r2 − r1|, r23 = |r3 − r2| and r13 = |r3 −r1|.
It should be mentioned that the full calculations of the two-body potential
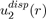
and threebody potential

allow us to generalize equations (15) and (16), respectively in the following forms:
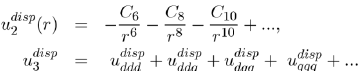
(17)
The various terms of these expressions have been calculated by the perturbation theory to fourth order, applied to the electronic structure of atoms. The details of these issues will be found in specialized articles [9], [10], [11].
Potentials in Liquid Rare Gases
Although the coefficients C6, C8, C10 in equation (17) are related to the energies of atoms, their values are only approximate. For example, for argon, they are:
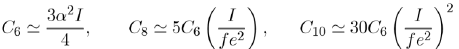
With a value of the atomic polarizability α = 1, 64.10−3 nm3 and an ionization potential of I = 17, 5 eV, the calculated value of C6 is worth about 9/10 of the experimental value. The values of the coefficients Ci are only approximate and the attractive potential in liquid rare gases are not rigorously defined. It is a matter of fact that the calculation of the repulsive potential is even more questionable. This explains why the construction of potentials in liquid rare gases is a combination of ab-initio and empirical calculations.
The first explicit calculation of the interaction between two helium atoms has been done by Slater and Kirkwood [12]. The resulting expression is the sum of a decay exponential function for the repulsive contribution and a power function varying as r−6 for the attractive contribution:
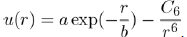
Where a,b and C6 are three constants. It is found that the repulsive interaction is of the BornMayer type (Eq. 1) and the attractive interaction is due to induced dipole-induced dipole dispersion forces (Eq. 15).
One of the most realistic two-body potentials for noble gases has been proposed by Aziz and Slaman[13] under the form:
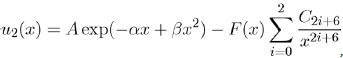
Where x = r/rm is the reduced distance and rm the position of the potential well. To eliminate the divergence introduced by the terms of dispersion to small distances, the authors have chosen to use the amortized function F(x):
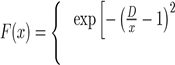
if x < D
if x ≥ D.
This potential model is composed of eight parameters determined by fitting some experimental quantities, the values of which will be found in the original article, for various rare gases. It should be noted that this potential is a pair potential and that the three-body Axilrod-Teller potential have to be added to improve the accuracy of calculation of the physical properties.
Law of Corresponding States
3.1 EMPIRICAL POTENTIAL
To facilitate the study of properties of liquids, it is desirable to use simpler expressions of the potential, although realistic, in order to simplify the analytical calculations. For example, the Gaussian potential is sometimes used to represent the repulsive part at short distance, because it facilitates the calculation of integrals that contain it. Also, the square-well potential:

(18)
Is widely used for its simple mathematical form. It correctly predicts the thermodynamic properties and the local structure of liquids. Without the square well, this potential reduces to the hard-sphere potential, which is also widely used.
There are a plethora of empirical potentials, but one that seems most appropriate to investigate the simple liquids is the Lennard-Jones potential. It is representative of many real potentials, insofar as it can describe numerous physical properties, without undue complexity of the calculations. Its general form is:
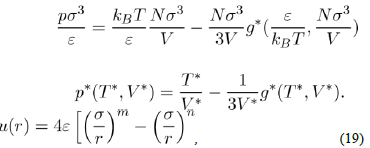
Where ε and σ are two parameters to be determined. The most commonly-used expression is that with n = 6 and m = 2n = 12. With a repulsive part varying as r−12 and an attractive part as r−6, it owns strong physical justification in view of equations (2) and (15). Moreover, the choice of the parametrization is particularly suited to the mathematical description of the function u(r). Indeed, σ is the value of r that makes the potential zero and ε is the depth of the potential well. By calculating the derivative
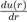
it is easy to see that the minimum position of the potential well is located at rm = 21/6σ, with u(rm) = −ε. The values of the parameters σ and ε are determined by fitting some experimental properties. They also allow estimating the coefficient C6(= 4εσ6). For argon, the value of C6 resulting of the empirical values of ε and σ is almost two times larger than the theoretical result.
Despite its limitations, the empirical potential of Lennard-Jones has a universal behavior favouring the study of many simple liquids, which differ from each other by the scale factors σi/ σj and εi/ εj. Indeed, it is reasonable to assume that the potential u(r) of each simple liquid can be represented in terms of a universal function u∗(r) as:
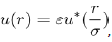
Which is typical of the Lennard-Jones potential.
Note that the equation of state of liquids is expressed by means of the configuration integral ZN(V,T), according to the equation:
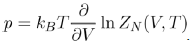
(20)
Using the expression for ZN (V,T), the pressure is given by the following equation[14]:
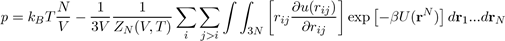
Where U (rN) = i j>i u (rij) is the potential energy of liquid consisting of N atoms. When the potential energy is assumed to be a sum of pair potentials of the universal type:
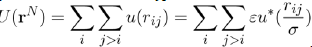
The pressure may be written in the functional form:

(21)
where
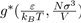
is a dimensionless function depending on the nature of the potential u∗, i.e. the parameters ε and σ. It follows that the pressure depends on the temperature T, the volume V and the universal function u∗, through the function g∗. However, if the two parameters ε and σ are used to define the reduced variables:
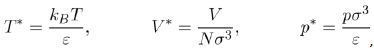
Equation (21) takes the reduced form:

This shows that the reduced pressure p∗ is a universal function of the reduced temperature T∗ and the reduced volume V ∗, for all the liquids described by a potential of the form

Equation (22) is known as the law of corresponding states stipulating that all the liquids of the same family, interacting with the potential u∗, obey the same equation of state in terms of reduced variables. As this reduced equation of state must apply to all the thermodynamic states, notably to the critical state, it is required that the values of and are universal constants for all the liquids described by the potential u∗. For the Lennard-Jones potential (12-6), the approximate values are
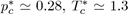
and
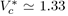
so that the product is equal to
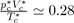
The experimental values of
figure
found for simple liquids [4] (Ar, Kr, Xe, N2, O2, CO2, CH4...) are about 0.290 ± 0.005, which yields an acceptable test of the theory.
Relationship between Potential and Limits of Phase Stability
One of the successes of numerical simulation has been to establish a relationship between the features of the interatomic potential and the limits of stability of phase diagrams, thus clarifying the circumstances of the liquid-solid and liquid-vapor transitions. It has been shown, in particular, that the hard-sphere potential is able to correctly describe the atomic structure of liquids and predict the liquid-solid transition [15], [16]. By contrast, it is unable to predict the liquid-vapor transition, which is due to the presence of attractive dispersion forces. More specifically, the simulation results have shown that the liquid-solid phase coexistence curves are governed by the repulsive part of potential, that is to say, by the steric hindrance of the atoms. This was already contained in the phenomenological theories of melting, like the Lindemann theory that predicts the melting of a solid when the average displacement of atoms, relatively to their equilibrium positions on the lattice, exceeds the atomic diameter of 10%. In other words, a substance melts when its volume exceeds by 30% the volume at 0 K.
Figure (4) displays the diagram p(T) of a pure substance as well as the Lennard-Jones potential (Eq. 19). One can see how the slope of the coexistence curve for solid-liquid phase varies with the repulsive part of the potential. Indeed, the greater the value of m, the steeper the repulsive part of the potential (Fig. 4b) and the less sloping the solid-liquid coexistence
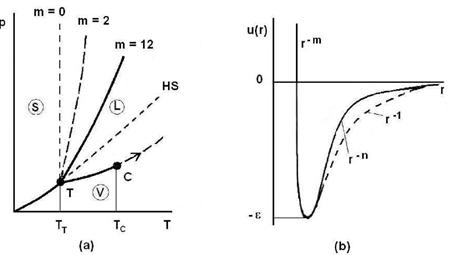
Figure 4: Schematic representations of the diagram p(T) and the Lennard-Jones potential.
Curve (Fig. 4a). Moreover, it becomes apparent that the Lennard-Jones potential predicts the liquid-vapor coexistence curve that begins at the triple point T and ends at the critical point C. A detailed analysis shows that the length of the segment TC is proportional to the depth of potential well ε. For rare gases, it is verified that (TC −TT)kB ≃ 0.55 ε. It follows immediately from this relation that the liquid-vapor coexistence curve disappears when the potential well is absent (ε = 0).
In addition, the value of the slope of the segment TC also depends on the attractive part of the potential as shown by the Clausius-Clapeyron equation:
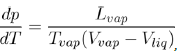
(23)
Where Lvap is the latent heat of vaporization at the corresponding temperature Tvap and (Vvap − Vliq) the difference of specific volumes between vapor and liquid. To evaluate the slope dTdp of TC, at ambient pressure, we can estimate the ratio
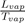
with Trouton’s rule (

J.K−1.mol−1) and the difference of volumes (Vvap −Vliq) in terms of width of the potential well. Indeed, noting that the quantity (Vvap−Vliq) is an increasing function of the width of potential well, which itself increases when n decreases, we remark that the value of the slope of the liquid-vapor coexistence curve decreases as n is decreasing, for a given well depth ε.
For liquid metals, it should be noted that the repulsive part of the potential is always softer than for liquid rare gases. Moreover, even if ε is slightly lower for metals than for rare gases, the report
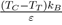
is much higher (between 2 and 4), which explains the elongation of the segment TC compared to that of rare gases. Also we mention that some flat-bottomed potentials [17], [18], [19] are likely to give a good description of the physical properties of elements having a low value of the ratio
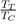
Such potentials are obviously not suitable for liquid rare gases, for which

or organic and inorganic liquids, for which 0
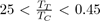
By contrast, they might be useful as empirical potentials for metals with low melting point, such as mercury, gallium, indium, tin, etc. with a ratio
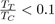
Weak Electron-Ion Interaction
4.1 The Schrödinger Equation
The atoms of rare gases considered in the preceding subsection have electronic shells completely filled. This ensures the stability of their electronic structures and allows treating the rare gases as liquids composed of single atoms. In contrast, the atoms in liquid metals have few electrons in the outer envelope - the valence band or s band. They are called the normal metals, such as alkali metals, which have a single electron in the s band. The easiness with which they can lose the valence electron gives them a high electronic conductivity. The polyvalent metals with several valence electrons are also assumed to be normal metals. In contrast, the noble metals and transition metals that possess, in addition to the valence electrons, a narrow d strip overlapping the s band cannot be treated like normal metals, because there are interactions (s-d hybridization) between s electrons and d electrons participating in conduction.
In normal metals, the conduction electrons, separated from ions, constitute a free electron gas that plays an active role in determining the energy of the system while the core electrons, tightly bound to nuclei, have no major impact. These considerations put forward by Drude, a century ago, suggest to consider the liquid metal as a mixture of ions interacting within the free electron gas and to write the energy E of the liquid metal as a sum of two terms:

(24)
Where the first term is the energy contribution that depends on the temperature and volume of N ions, and the second term is the energy contribution depending, in addition, on the configuration of ions in positions Ri. It will be seen later that this contribution can be written as the sum of effective pair potentials:
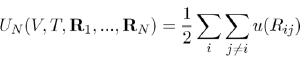
(25)
Between entities (pseudoions), which differ noticeably from the genuine ions. The sum i j=i and the factor 1/2 come from the fact that the interaction between a pair of particles should not be counted twice. The effective potential u (Rij) has a functional form that depends on the volume and the temperature, as well as on the capacity of the electron gas to screen the ions.
The calculation of the energy E is a complicated problem of quantum mechanics solved by the perturbation theory to second order of the pseudopotential, i.e. the interaction between an electron and an ion
Since a liquid metal is considered as a set of ions of charge Ze (where Z is the valence), imbedded in the free electron gas, its dynamic state can be described owing to the Schrödinger equation:

(26)
Where H is the Hamiltonian of the system, ψ the wave function and E the energy. The Hamiltonian operator H contains all the forms of energy such as kinetic energies of the free electrons and ions:
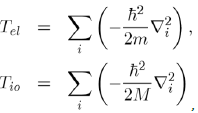
And potential energies of the electron-electron, ion-ion and electron-ion interactions:

(27)
In such a scheme, the ions of mass M have coordinates Rα and the free electrons of charge e and mass m have coordinates ri.
To solve the Schrödinger equation (Eq. 26), it is essential to reduce the system of (Z +1) N particles into interaction to a system of independent particles, with reasonable simplifications, this in order to write the wave function ψ of the system as a product of wave functions of all the particles and the total energy E as a sum of energies The first simplification (adiabatic approximation) takes into account the difference between the masses of the electrons and ions. The assumption made here is to admit that the ions are heavier and immobile with respect to the electrons whose movements are much faster With this simplification, the ion-ion interaction energy Uio−io must be calculated separately and added to the electronic energy Eel coming from the electronic Schrödinger equation [1] Indeed, the metal is composed of N ions and NZ free electrons. [2] The adiabatic approximation, known as the Born-Oppenheimer approximation, is usually presented in a more subtile manner, but the supposition that the ions are fixed affects very little the results of the energy calculation.
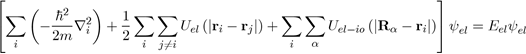
(28)
Where ψel represents the wave function of the electrons in presence of the ions.A second simplification is needed to solve the above equation, which is not yet related to a single electron because of the double sum on i and j in the term i j=i Uel (|ri − rj|). Obviously, equation (28), describing the state of ZN electrons interacting in the presence of the ions, could be reduced to an equation for one electron if there was no interaction between electrons (Uel = 0) since the Hamiltonian would be decomposed into a sum of ZN Hamiltonians. In the case of a system of interacting electrons, the reduction of equation (28) is however possible through the Hartree approximation. The latter consists in (1) approximating the many-electron wave function ψel as a product of single-particle functions:
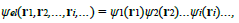
And (2) replacing the energy of electron-electron interaction, Uel−el, by a function - the Hartree potential WH (ri) - representing the potential energy of the electron i in the field of all the other electrons:
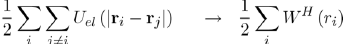
Where the Hartree potential satisfies the Poisson equation4:
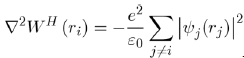
The expression of WH (ri) is:
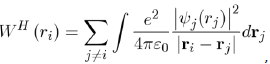
Where its physical meaning is as follows: (1)
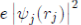
represents the charge density of the Electron cloud produced by the electron j, (2) the quantity
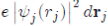
is the electric charge Of the volume element drj and (3) the integral
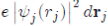
is the interaction energy of the electron i with the electron j. Note that the potential energy WH (ri) of the electron i depends not only on the movements of all the other electrons but, indirectly, on its own motion, which consequently influences the movements of the other electrons. In view of this, the function WH (ri) determines not only the motion of the electron i but also depends on it. The determination of the function WH (ri) is made, in principle, in a self-consistent manner by iterative calculations.
Thus, the implementation of the Hartree approximation enables us to write the Hamiltonian of equation (28) as:
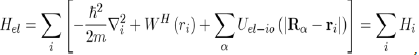
And to reduce the Schrödinger equation for multiple electrons (Eq. 28) to the equation for a single electron:
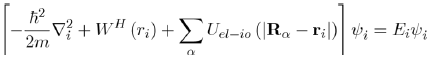
(29)
Where the wave function of the system ψel is equal to the product of the single wave functions

and the electronic energy of the system is equal to the sum of the energies of each electron

It should be mentioned that the Fermi statistics can be incorporated into the Hartree approximation in replacing the product of single wave functions by orbitals under the form of a Slater determinant. This new scheme, known as the Hartree-Fock approximation, leads to an additional term in the Schrödinger equation taking account of the exchange effects, which improves the total energy computation. Note that the correlation effects can also be included in the calculations. In the following, we will introduce the exchange and correlation effects through the screening and pseudopotential theories, without resorting to the Hartree-Fock approximation.
4The Poisson and Coulomb equations are written in the rationalized M.K.S. unit system (SI units) as ∇2Φ(r) ∝

and
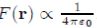
Concept of Pseudopotential
The two foregoing simplifications have been made to reduce the study of liquid metals to that of an independent electron. But the resolution of equation (29) is not yet possible because the electron-ion interaction energy Uel−io(r) and the Hartree potential WH (r) are unknown functions
Consider first the potential of electron-ion interaction. If the electron i is close to the ion α, the most important energy contribution is provided by the electrostatic potential between the electrons i and the ion α (Fig. 5). This potential has a deep well surrounding the ion and varies as 1/r when the electron moves away. Regarding the interactions between the electrons i and all the other ions, they are very weak when the distance separating them is large. Thus they provide no significant contribution to the energy Ei, so that the dominant feature of the sum sum α Uel−io (|Rα − ri|) is to depend only on the interaction between the electron i and the nearest ion.
To solve the Schrödinger equation for one electron (Eq. 29), the perturbation theory independent of time is required. This method can be implemented only when the potential energy operator is small enough to be treated as a perturbation. However, this is not the case because of the divergence of the potential α Uel−io (|Rα − ri|) for ri ≃ Rα. To by-pass this difficulty, the true wave function ψi is replaced by a pseudofunction χi, smooth on the outside and the inside of the ion, with the aim of transforming the potential energy operator, α Uel−io (|Rα − ri|), into a pseudopotential W0 (r) = α w0 (|Rα − ri|) sufficiently small everywhere to justify the use of the perturbation theory.
The pseudopotential theory proposed by Phillips and Kleinman[1] is based on theoretical foundations that will not be discussed here. In turn, we provide a justification to the fact that the pseudopotential W0 (r) is small throughout the system, and give a simple analytical expression for the individual pseudopotential w0(r) based on the following arguments. As already mentioned, the potential felt by the electron i in the vicinity of the ion α is a Coulomb potential equal to But the electron i is also subjected to a repulsive potential generated by the core electrons of the ion α due to the Pauli exclusion principle, which can be represented by a Dirac peak +λδ(|Rα − ri| given the small size of ions. Therefore, in the vicinity of an ion, the pseudopotential w0(r) may be taken to be the sum of these two contributions (Fig. 5) using, for instance, the representation of the analytical model of Ashcroft [20]:

(30)
In this model, it is assumed that the repulsive potential cancels completely the attractive potential in a sphere of radius Rc to be determined. Obviously, there are models in which the potential in the core is not zero. Some, like that of Ashcroft, has a simple analytical form. Others are operators (non-local pseudopotentials) and, therefore, have no simple analytical form [21], [22], [23], [24]. All calculations presented in the sequel will be made with the Ashcroft local pseudopotential.
If it is accepted that a low pseudopotential W0 (r) exists, the problem of one free electron in the collection of the ions and other electrons might be then solved. To do this, we rewrite equation (29) with the pseudopotential W0 (r) and the pseudo wave function χk(r), in removing
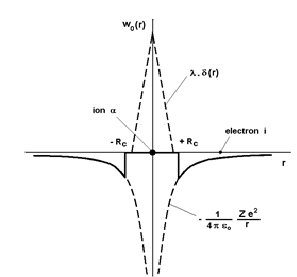
Figure 5: Analytical model of the Ashcroft pseudopotential
The index i and using the classical notations of quantum mechanics 3:
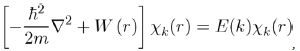
(31)
with W(r) = WH (r) + W0 (r).
Then, the electronic energy E(k) may be determined with the perturbation theory by adopting the free electron model as zero order approximation. This model states that the Schrödinger equation of one free electron in a box of volume V is written:
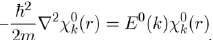
It is found that this equation admits a solution under the form of a plane wave:
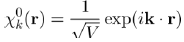
(33)
And has an energy spectrum given by:

(34)
Thus, in the zero order approximation, the energy of one free electron E0 (k) varies continuously with the square of the wave vector k. Moreover, the electronic energy of the system composed of NZ free electrons is:

(35 )
Where
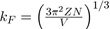
is the wave vector at the Fermi level.

Form factor, structure factor and electron energy
5.1 Perturbation theory for non-degenerate states
The perturbation theory aims to determine the corrections to the energy E0 (k) and wave function χ0k(r) of the free electron system, when a perturbation W (r) (Eq. 32) is imposed. In this section, we briefly describe the time independent perturbation theory to second order 4 for non-degenerate states, because it is the only useful result here.
Consider the unperturbed quantum system governed by the Schrödinger equation:
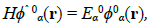
(36)
Where the discrete spectrum of eigenvalues and eigen functions of the Hamiltonian Hˆ are assumed to be known. As the quantum states are not degenerate, only one wave function corresponds to each value of energy. In what follows, it is proposed to determine the approximate solutions of the wave function ψβ(r) and energy Eβ of the quantum system subjected to the weak perturbation Wˆ, whose equation Schrödinger is:

(37)
Where λ is a parameter primarily used to facilitate the analysis. It takes the value 0 when the system is not perturbed and 1 when the system is perturbed. To find the solution of this equation, use is made of the Dirac prescription that consists in expanding the unknown wave function ψβ(r) on the basis of the eigenwave functions ϕ0α(r), namely:
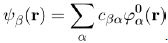
(38)
This expansion is then substituted in equation (37):
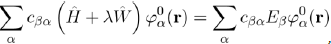
Which, with equation (36), may be put in the form:

And after simplifications7, this relation becomes:

(39)
Multiply now the left hand side by and integrate over the domain concerned. The result is:
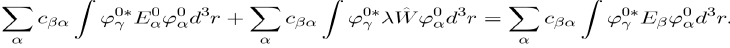
(40)
The perturbation theory sets itself as a goal to seek the energy Eβ and the coefficients cβα, likely to solve equation (37), under the series expansions:

(41)
Where the quantities Eβ0 and c0βα correspond to the unperturbed system (zero order approximation), Eβ (1) and c (1) βα to the first order corrections, etc. By inserting the previous expansions in equation (39), it comes:

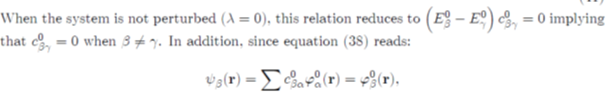

To determine the first order correction of the perturbed system, we neglect the powers of λ greater than or equal to two in equation (41) and take λ = 1:
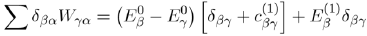

Since the base formed by the eigenfunctionsis orthonormal, the three terms of the previous equation are reduced, respectively, to:

Where
is the matrix element of the perturbation.
With these conditions in mind, the first order approximation of the energy Eβ (Eq. 40) and wave function ψβ(r) (Eq. 38) of the perturbed system are written:
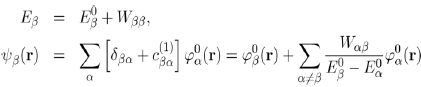
(43)
Then, to determine the second order correction of the perturbed system, we ignore the powers of λ greater than or equal to three in equation (41) and take λ = 1:
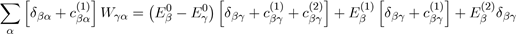
In the case where γ = β with β = α, for which Eβ (1) = 0, the above relation reduces to:
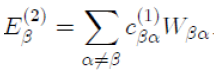
Now, in substituting
in the previous equation, with the help of equation (42), we obtain the energy to second order:
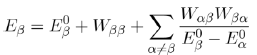
(44)
Factorization of the matrix elements
In the study of liquid metals, it is not necessary to go beyond the approximations to second order for the energy (Eq. 44) and first order for the wave function (Eq. 43). Consequently, the energy E(k) and the wave function χk(r) of one conduction electron, in the system subjected to the perturbation W(r), can be evaluated in rewriting equations (44) and (43) with the notations for the energy and the matrix element of the perturbation adapted to the problem:

(45,46)
Where the first terms of these series correspond to the energy and the wave function of the free electron model (Eqs. 33 and 34), while the corrective terms depend on the matrix element:
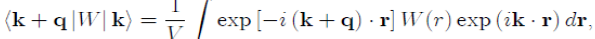
(47)
Which is responsible for the diffusion over a surface of constant energy. Indeed, k + q|W|k is the expression of the diffusion of a conduction electron from the initial state defined by the wave vector k to the final state k′ = k+q, by the total pseudopotential W(r) weakly scattering. Since the matrix element must be calculated with the pseudopotential W0(r) of the bare ion plus the Hartree potential WH (r) (Eq. 32), the total potential W(r) is written as a sum of individual pseudopotentials centered on the ions, under the form :

(48)
Finally, the expression of the matrix element is found in inserting equation (48) in equation (47):

Since (Rα − r) is a dummy variable, we pose X = r − Rα in order to achieve the factorization of the matrix element as:
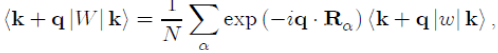
(49)
With:
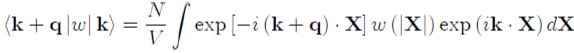
(50)
It should be stressed that the square of the matrix element in equation (45) is usually written as:
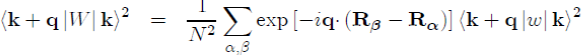
(51)
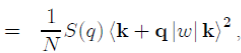
(52)
where k + q|w|k is the form factor resulting from the individual potential of the ion and S(q) the ionic structure factor, which depends on the position of the ions and can be directly measured by X-ray or neutron scattering. Its definition is:
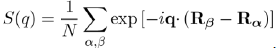
In the framework of the perturbation theory briefly presented, it is found that the electron energy Eel of a metal is equal to the sum of the energies E(k) of all the free electrons. In practice, the perturbation theory performs the calculations in the reciprocal space and not in the direct space. Therefore, the electronic energy Eel is calculated in k-space in doing the sum of all the energy states occupied in the Fermi sphere of radius kF , with the expression9:

Where E (k) is given by equation (45). The electron energy Eel of a metal may thus be put under the form10:
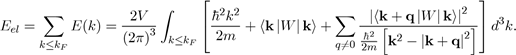
(53)
Screening theory in the Hartree approximation
6.1 Form factor of the Ashcroft pseudopotential
As a rough guide, the form factor of Ashcroft’s pseudopotential w0 (r) will be calculated by substituting equation (30) in equation (50):
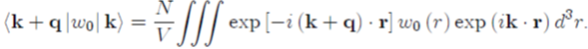
The integration in the above relation is better carried out with the spherical coordinates
d3r = r2 sinθdθdϕdr,
And qr = qrcosθ,
After placing the vectors q and r as shown in figure (6). With this change of variables, the form factor becomes:
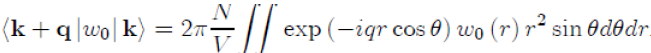
To perform the integration on the variable θ, we take µ = cosθ ranging from 1 to −1, with dµ = −sinθdθ,whichgives:
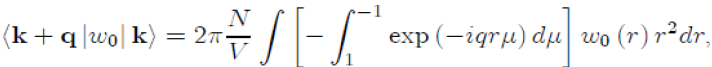
9The transformation of the discrete sum into an integral over k is done by using the formula:

The number of electrons in the unit volume of the k-space is
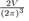
However, for a free electron system, the volume occupied by the electrons in k-space is a sphere of radius kF, called the Fermi sphere. Therefore, the number of free electrons NZ is the product of the number of electrons per unit volume multiplied by the volume of the Fermi sphere:
hence
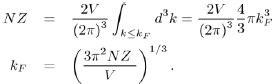
10 From now, it is important to note that the energy Eel does not correspond exactly to the electronic energy of the metal because, to perform its calculation, the electron-electron energy is counted twice. Therefore, the latter should be subtracted at any time.

Figure 6: Positions of the vectors q and r to calculate the form factor w0 (q).
Where the integral in square brackets is:
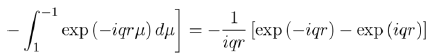
(54)
Before performing the integration over r, we replace the pseudopotential by its expression (Eq. 30) and introduce the damping factor exp(−αr) that will disappear at the end of the calculation by letting α go toward zero, as follows:
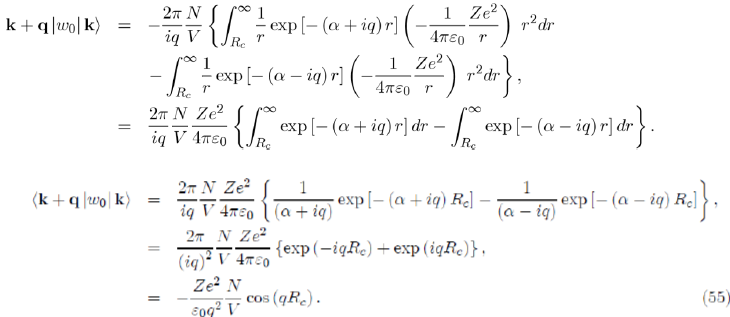
Matrix Element of the Hartree Potential
In the preceding subsections, the expression of the electronic energy
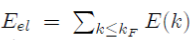
of metals has been derived as a function of E (k) (Eq. 53). The energy E(k) is the energy of one given conduction electron in interaction with the ions and the other electrons of the system, and it depends on the total pseudopotential W(r) = WH (r) + W0(r) via the matrix element k + q|W|k (Eq. 47). However, this matrix element is only partially known. Indeed, there is an expression for the matrix element k + q|W0|k of the bare pseudopotential (Eq. 55), but not any for the matrix element k + q WH k! Containing the electron-electron interactions in the Hartree approximation.
To find the expression of the matrix element k + q WH k!, use is made of the screening theory[25] based on the concept of dielectric function. The principle of the method is to deterk + q|W|k = k + q WH k! + k + q|W0|k as a function of the electronic cloud density! Mine, in a self-consistent manner, the matrix element k + q WH k and the matrix element
n(r). The method consists of calculating the electron density with the wave function (first postulate of quantum mechanics) by jointly using the Poisson equation. Thus, the electron density n(r) is given by the sum, over all occupied states in the Fermi sphere, of the product of the pseudo wave functions χk(r) (Eq. 46) by its complex conjugate
, that is to say:
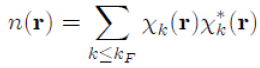
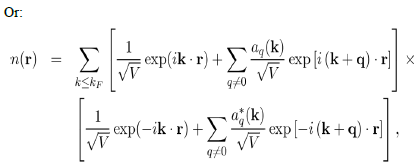
Where it has been written:

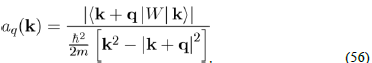
So that the total electron density is:
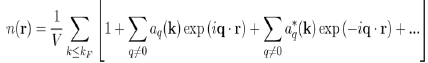
The constant term corresponds to the uniform distribution of negative charge that compensates the positive charge of the ions. And the remaining terms represent the oscillating charge density, screening the ions, which is directly related to the Hartree potential WH(r) by Poisson’s equation. By neglecting the terms of the expansion to the higher order than one, in the pseudo wave function, the oscillating electronic density nosc(r) reduces to:
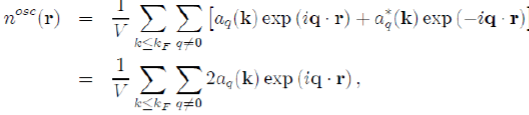
(57)
Because
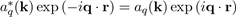
by the definition of aq(k).
As far as Poisson’s equation

is concerned, where Φ(r) is the electrostatic potential, it is rewritten with the Hartree potential WH(r) = eΦ(r) as:
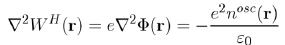
(58)
To implement the method, it is easier to combine equations (57) and (58) after performing The standard transformations in k-space11:
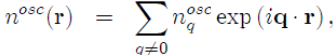
(59)

(60)
By comparing equations (57) and (59), and by calculating the Laplacian of WH(r) with equation (60), we obtain the following relations:
The insertion of these expressions into equation (58) enables us to write the Poisson equation under the algebraic form:
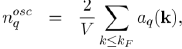
(61)
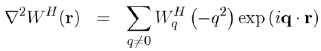
(62)
The Hartree potential WqH is then written explicitly in terms of the matrix element | k + q|W|k|, by using equations (61) and (56):

From which we arrive at the following final expression, by taking account of the formula given in footnote 9:

(63)
Concept of Dielectric Function
In order to pursue the calculation of the Hartree potential (Eq. 63) without too much difficulty, assume that the pseudopotential is local. It therefore follows that the matrix element
11The transformation of the discrete sum into an integral over q is done by using the formula:
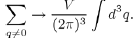
This allows us to define the Fourier transform:
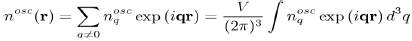
With It is the same for the function
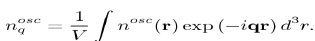
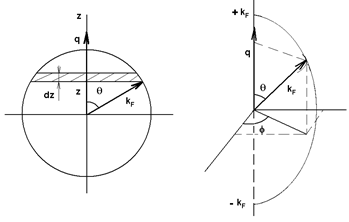
Figure 7: Choice of the integration variables for calculating the integral in equation (64), into the Fermi sphere. The shaded area corresponds to the volume element d3k
| k + q|W|k| depends only on q and can be extracted from the integral over k, which is not the case in the complete theory [23], [26], [27]. The calculation of

is thus reduced to that of the integral:
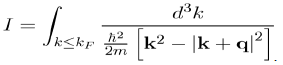
(64)
To achieve the integration over the states contained in the Fermi sphere, the sphere of radius kF is first drawn, then the transfer vector q is placed along the z-axis (Fig. 7) and the following change of variables is performed:
So that the element of integration is the disc of volume:
d3k = π kF2 − z2 dz.
Clearly Auctoresonline and particularly Psychology and Mental Health Care Journal is dedicated to improving health care services for individuals and populations. The editorial boards' ability to efficiently recognize and share the global importance of health literacy with a variety of stakeholders. Auctoresonline publishing platform can be used to facilitate of optimal client-based services and should be added to health care professionals' repertoire of evidence-based health care resources.

Journal of Clinical Cardiology and Cardiovascular Intervention The submission and review process was adequate. However I think that the publication total value should have been enlightened in early fases. Thank you for all.

Journal of Women Health Care and Issues By the present mail, I want to say thank to you and tour colleagues for facilitating my published article. Specially thank you for the peer review process, support from the editorial office. I appreciate positively the quality of your journal.
Journal of Clinical Research and Reports I would be very delighted to submit my testimonial regarding the reviewer board and the editorial office. The reviewer board were accurate and helpful regarding any modifications for my manuscript. And the editorial office were very helpful and supportive in contacting and monitoring with any update and offering help. It was my pleasure to contribute with your promising Journal and I am looking forward for more collaboration.

We would like to thank the Journal of Thoracic Disease and Cardiothoracic Surgery because of the services they provided us for our articles. The peer-review process was done in a very excellent time manner, and the opinions of the reviewers helped us to improve our manuscript further. The editorial office had an outstanding correspondence with us and guided us in many ways. During a hard time of the pandemic that is affecting every one of us tremendously, the editorial office helped us make everything easier for publishing scientific work. Hope for a more scientific relationship with your Journal.

The peer-review process which consisted high quality queries on the paper. I did answer six reviewers’ questions and comments before the paper was accepted. The support from the editorial office is excellent.

Journal of Neuroscience and Neurological Surgery. I had the experience of publishing a research article recently. The whole process was simple from submission to publication. The reviewers made specific and valuable recommendations and corrections that improved the quality of my publication. I strongly recommend this Journal.

Dr. Katarzyna Byczkowska My testimonial covering: "The peer review process is quick and effective. The support from the editorial office is very professional and friendly. Quality of the Clinical Cardiology and Cardiovascular Interventions is scientific and publishes ground-breaking research on cardiology that is useful for other professionals in the field.

Thank you most sincerely, with regard to the support you have given in relation to the reviewing process and the processing of my article entitled "Large Cell Neuroendocrine Carcinoma of The Prostate Gland: A Review and Update" for publication in your esteemed Journal, Journal of Cancer Research and Cellular Therapeutics". The editorial team has been very supportive.

Testimony of Journal of Clinical Otorhinolaryngology: work with your Reviews has been a educational and constructive experience. The editorial office were very helpful and supportive. It was a pleasure to contribute to your Journal.

Dr. Bernard Terkimbi Utoo, I am happy to publish my scientific work in Journal of Women Health Care and Issues (JWHCI). The manuscript submission was seamless and peer review process was top notch. I was amazed that 4 reviewers worked on the manuscript which made it a highly technical, standard and excellent quality paper. I appreciate the format and consideration for the APC as well as the speed of publication. It is my pleasure to continue with this scientific relationship with the esteem JWHCI.

This is an acknowledgment for peer reviewers, editorial board of Journal of Clinical Research and Reports. They show a lot of consideration for us as publishers for our research article “Evaluation of the different factors associated with side effects of COVID-19 vaccination on medical students, Mutah university, Al-Karak, Jordan”, in a very professional and easy way. This journal is one of outstanding medical journal.
Dear Hao Jiang, to Journal of Nutrition and Food Processing We greatly appreciate the efficient, professional and rapid processing of our paper by your team. If there is anything else we should do, please do not hesitate to let us know. On behalf of my co-authors, we would like to express our great appreciation to editor and reviewers.

As an author who has recently published in the journal "Brain and Neurological Disorders". I am delighted to provide a testimonial on the peer review process, editorial office support, and the overall quality of the journal. The peer review process at Brain and Neurological Disorders is rigorous and meticulous, ensuring that only high-quality, evidence-based research is published. The reviewers are experts in their fields, and their comments and suggestions were constructive and helped improve the quality of my manuscript. The review process was timely and efficient, with clear communication from the editorial office at each stage. The support from the editorial office was exceptional throughout the entire process. The editorial staff was responsive, professional, and always willing to help. They provided valuable guidance on formatting, structure, and ethical considerations, making the submission process seamless. Moreover, they kept me informed about the status of my manuscript and provided timely updates, which made the process less stressful. The journal Brain and Neurological Disorders is of the highest quality, with a strong focus on publishing cutting-edge research in the field of neurology. The articles published in this journal are well-researched, rigorously peer-reviewed, and written by experts in the field. The journal maintains high standards, ensuring that readers are provided with the most up-to-date and reliable information on brain and neurological disorders. In conclusion, I had a wonderful experience publishing in Brain and Neurological Disorders. The peer review process was thorough, the editorial office provided exceptional support, and the journal's quality is second to none. I would highly recommend this journal to any researcher working in the field of neurology and brain disorders.

Dear Agrippa Hilda, Journal of Neuroscience and Neurological Surgery, Editorial Coordinator, I trust this message finds you well. I want to extend my appreciation for considering my article for publication in your esteemed journal. I am pleased to provide a testimonial regarding the peer review process and the support received from your editorial office. The peer review process for my paper was carried out in a highly professional and thorough manner. The feedback and comments provided by the authors were constructive and very useful in improving the quality of the manuscript. This rigorous assessment process undoubtedly contributes to the high standards maintained by your journal.

International Journal of Clinical Case Reports and Reviews. I strongly recommend to consider submitting your work to this high-quality journal. The support and availability of the Editorial staff is outstanding and the review process was both efficient and rigorous.

Thank you very much for publishing my Research Article titled “Comparing Treatment Outcome Of Allergic Rhinitis Patients After Using Fluticasone Nasal Spray And Nasal Douching" in the Journal of Clinical Otorhinolaryngology. As Medical Professionals we are immensely benefited from study of various informative Articles and Papers published in this high quality Journal. I look forward to enriching my knowledge by regular study of the Journal and contribute my future work in the field of ENT through the Journal for use by the medical fraternity. The support from the Editorial office was excellent and very prompt. I also welcome the comments received from the readers of my Research Article.

Dear Erica Kelsey, Editorial Coordinator of Cancer Research and Cellular Therapeutics Our team is very satisfied with the processing of our paper by your journal. That was fast, efficient, rigorous, but without unnecessary complications. We appreciated the very short time between the submission of the paper and its publication on line on your site.

I am very glad to say that the peer review process is very successful and fast and support from the Editorial Office. Therefore, I would like to continue our scientific relationship for a long time. And I especially thank you for your kindly attention towards my article. Have a good day!

"We recently published an article entitled “Influence of beta-Cyclodextrins upon the Degradation of Carbofuran Derivatives under Alkaline Conditions" in the Journal of “Pesticides and Biofertilizers” to show that the cyclodextrins protect the carbamates increasing their half-life time in the presence of basic conditions This will be very helpful to understand carbofuran behaviour in the analytical, agro-environmental and food areas. We greatly appreciated the interaction with the editor and the editorial team; we were particularly well accompanied during the course of the revision process, since all various steps towards publication were short and without delay".

I would like to express my gratitude towards you process of article review and submission. I found this to be very fair and expedient. Your follow up has been excellent. I have many publications in national and international journal and your process has been one of the best so far. Keep up the great work.

We are grateful for this opportunity to provide a glowing recommendation to the Journal of Psychiatry and Psychotherapy. We found that the editorial team were very supportive, helpful, kept us abreast of timelines and over all very professional in nature. The peer review process was rigorous, efficient and constructive that really enhanced our article submission. The experience with this journal remains one of our best ever and we look forward to providing future submissions in the near future.

I am very pleased to serve as EBM of the journal, I hope many years of my experience in stem cells can help the journal from one way or another. As we know, stem cells hold great potential for regenerative medicine, which are mostly used to promote the repair response of diseased, dysfunctional or injured tissue using stem cells or their derivatives. I think Stem Cell Research and Therapeutics International is a great platform to publish and share the understanding towards the biology and translational or clinical application of stem cells.

I would like to give my testimony in the support I have got by the peer review process and to support the editorial office where they were of asset to support young author like me to be encouraged to publish their work in your respected journal and globalize and share knowledge across the globe. I really give my great gratitude to your journal and the peer review including the editorial office.

I am delighted to publish our manuscript entitled "A Perspective on Cocaine Induced Stroke - Its Mechanisms and Management" in the Journal of Neuroscience and Neurological Surgery. The peer review process, support from the editorial office, and quality of the journal are excellent. The manuscripts published are of high quality and of excellent scientific value. I recommend this journal very much to colleagues.

Dr.Tania Muñoz, My experience as researcher and author of a review article in The Journal Clinical Cardiology and Interventions has been very enriching and stimulating. The editorial team is excellent, performs its work with absolute responsibility and delivery. They are proactive, dynamic and receptive to all proposals. Supporting at all times the vast universe of authors who choose them as an option for publication. The team of review specialists, members of the editorial board, are brilliant professionals, with remarkable performance in medical research and scientific methodology. Together they form a frontline team that consolidates the JCCI as a magnificent option for the publication and review of high-level medical articles and broad collective interest. I am honored to be able to share my review article and open to receive all your comments.

“The peer review process of JPMHC is quick and effective. Authors are benefited by good and professional reviewers with huge experience in the field of psychology and mental health. The support from the editorial office is very professional. People to contact to are friendly and happy to help and assist any query authors might have. Quality of the Journal is scientific and publishes ground-breaking research on mental health that is useful for other professionals in the field”.

Dear editorial department: On behalf of our team, I hereby certify the reliability and superiority of the International Journal of Clinical Case Reports and Reviews in the peer review process, editorial support, and journal quality. Firstly, the peer review process of the International Journal of Clinical Case Reports and Reviews is rigorous, fair, transparent, fast, and of high quality. The editorial department invites experts from relevant fields as anonymous reviewers to review all submitted manuscripts. These experts have rich academic backgrounds and experience, and can accurately evaluate the academic quality, originality, and suitability of manuscripts. The editorial department is committed to ensuring the rigor of the peer review process, while also making every effort to ensure a fast review cycle to meet the needs of authors and the academic community. Secondly, the editorial team of the International Journal of Clinical Case Reports and Reviews is composed of a group of senior scholars and professionals with rich experience and professional knowledge in related fields. The editorial department is committed to assisting authors in improving their manuscripts, ensuring their academic accuracy, clarity, and completeness. Editors actively collaborate with authors, providing useful suggestions and feedback to promote the improvement and development of the manuscript. We believe that the support of the editorial department is one of the key factors in ensuring the quality of the journal. Finally, the International Journal of Clinical Case Reports and Reviews is renowned for its high- quality articles and strict academic standards. The editorial department is committed to publishing innovative and academically valuable research results to promote the development and progress of related fields. The International Journal of Clinical Case Reports and Reviews is reasonably priced and ensures excellent service and quality ratio, allowing authors to obtain high-level academic publishing opportunities in an affordable manner. I hereby solemnly declare that the International Journal of Clinical Case Reports and Reviews has a high level of credibility and superiority in terms of peer review process, editorial support, reasonable fees, and journal quality. Sincerely, Rui Tao.

Clinical Cardiology and Cardiovascular Interventions I testity the covering of the peer review process, support from the editorial office, and quality of the journal.

Clinical Cardiology and Cardiovascular Interventions, we deeply appreciate the interest shown in our work and its publication. It has been a true pleasure to collaborate with you. The peer review process, as well as the support provided by the editorial office, have been exceptional, and the quality of the journal is very high, which was a determining factor in our decision to publish with you.
The peer reviewers process is quick and effective, the supports from editorial office is excellent, the quality of journal is high. I would like to collabroate with Internatioanl journal of Clinical Case Reports and Reviews journal clinically in the future time.

Clinical Cardiology and Cardiovascular Interventions, I would like to express my sincerest gratitude for the trust placed in our team for the publication in your journal. It has been a true pleasure to collaborate with you on this project. I am pleased to inform you that both the peer review process and the attention from the editorial coordination have been excellent. Your team has worked with dedication and professionalism to ensure that your publication meets the highest standards of quality. We are confident that this collaboration will result in mutual success, and we are eager to see the fruits of this shared effort.

Dear Dr. Jessica Magne, Editorial Coordinator 0f Clinical Cardiology and Cardiovascular Interventions, I hope this message finds you well. I want to express my utmost gratitude for your excellent work and for the dedication and speed in the publication process of my article titled "Navigating Innovation: Qualitative Insights on Using Technology for Health Education in Acute Coronary Syndrome Patients." I am very satisfied with the peer review process, the support from the editorial office, and the quality of the journal. I hope we can maintain our scientific relationship in the long term.
Dear Monica Gissare, - Editorial Coordinator of Nutrition and Food Processing. ¨My testimony with you is truly professional, with a positive response regarding the follow-up of the article and its review, you took into account my qualities and the importance of the topic¨.

Dear Dr. Jessica Magne, Editorial Coordinator 0f Clinical Cardiology and Cardiovascular Interventions, The review process for the article “The Handling of Anti-aggregants and Anticoagulants in the Oncologic Heart Patient Submitted to Surgery” was extremely rigorous and detailed. From the initial submission to the final acceptance, the editorial team at the “Journal of Clinical Cardiology and Cardiovascular Interventions” demonstrated a high level of professionalism and dedication. The reviewers provided constructive and detailed feedback, which was essential for improving the quality of our work. Communication was always clear and efficient, ensuring that all our questions were promptly addressed. The quality of the “Journal of Clinical Cardiology and Cardiovascular Interventions” is undeniable. It is a peer-reviewed, open-access publication dedicated exclusively to disseminating high-quality research in the field of clinical cardiology and cardiovascular interventions. The journal's impact factor is currently under evaluation, and it is indexed in reputable databases, which further reinforces its credibility and relevance in the scientific field. I highly recommend this journal to researchers looking for a reputable platform to publish their studies.

Dear Editorial Coordinator of the Journal of Nutrition and Food Processing! "I would like to thank the Journal of Nutrition and Food Processing for including and publishing my article. The peer review process was very quick, movement and precise. The Editorial Board has done an extremely conscientious job with much help, valuable comments and advices. I find the journal very valuable from a professional point of view, thank you very much for allowing me to be part of it and I would like to participate in the future!”

Dealing with The Journal of Neurology and Neurological Surgery was very smooth and comprehensive. The office staff took time to address my needs and the response from editors and the office was prompt and fair. I certainly hope to publish with this journal again.Their professionalism is apparent and more than satisfactory. Susan Weiner

My Testimonial Covering as fellowing: Lin-Show Chin. The peer reviewers process is quick and effective, the supports from editorial office is excellent, the quality of journal is high. I would like to collabroate with Internatioanl journal of Clinical Case Reports and Reviews.

My experience publishing in Psychology and Mental Health Care was exceptional. The peer review process was rigorous and constructive, with reviewers providing valuable insights that helped enhance the quality of our work. The editorial team was highly supportive and responsive, making the submission process smooth and efficient. The journal's commitment to high standards and academic rigor makes it a respected platform for quality research. I am grateful for the opportunity to publish in such a reputable journal.
My experience publishing in International Journal of Clinical Case Reports and Reviews was exceptional. I Come forth to Provide a Testimonial Covering the Peer Review Process and the editorial office for the Professional and Impartial Evaluation of the Manuscript.
