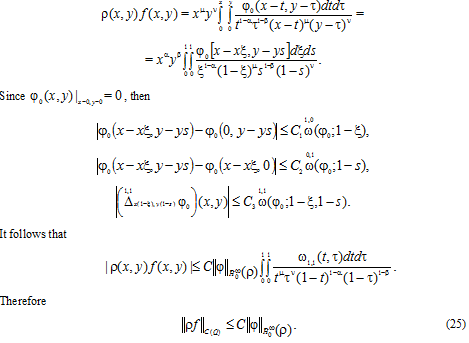In the presented work for operators the mixed fractional integration character of improvement of smoothness in comparison with smoothness of density  

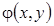
  with weight  

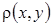
 in case of its any continuity modulus is found out 

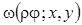
 Zygmund type estimates are received. We consider operators of mixed fractional integration in weighted generalized Hölder spaces of a function of two variables defined by a mixed modulus of continuity.

One of the most important problems in the theory of integral operators in space is the problem of elucidating the dependence of the smoothness of the image on the smoothness of the preimage. The solution to such a problem plays an important role in the solvability of integral equations, their stability, and so on. The concept of smoothness can be formulated in a variety of terms. One of the ways of sufficiently fine-grabbing the smoothness of functions is the notion of generalized Hölderness, formulated in terms of the behavior of the modulus of continuity. Thus, one of the important questions in the theory of operators is as follows: Let be A an operator acting in a Banach space X and let be the modulus of continuity 

  of

 X. How can the behavior of the modulus of continuity be characterized  

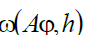
 if the behavior of the modulus of continuity of function 

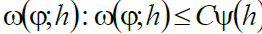
  for all is known   

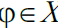
   where is  

  a given continuous function  

This problem admits a natural generalization to the weight case namely, let  

  weight function and  

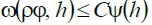
 for all  

  How to estimate the modulus of continuity  

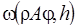
  A similar problem can be considered completely solved for different spaces, and also for the Holder space of functions of one variable and power weights, when  

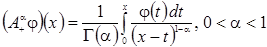
    ([2] – [6], [13] – [19]). A detailed review of these and some other close results can be found in [12].

The assertion for multidimensional cases on the property of mapping in the usual Hölder and in the Hölder spaces defined by mixed differences are known [7], [8], [9], [10], [11], [12].

A similar problem in generalized Hölder spaces of the function of several variables has not been studied. This paper is aimed to fill in this gap. We deal with both non-weighted and weighted spaces.

An important stage in the study of fractional integro-differentiation of functions from generalized Hölder spaces (see [1] - [6], [13], [14], [18]) is obtaining estimates of Zygmund type; Estimate of the modulus of continuity of a fractional integral in terms of the modulus of continuity of the original function.

  The main thrust of the work is to obtain an estimate of the Zygmund type that majorizes the mixed modulus 

  of continuity of a mixed fractional integral with the weight of integral constructions from the mixed modulus of continuity  

 of its density  

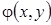
   with weight  

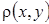
  These Zygmund-type estimates and action theorems directly affect the character of the improvement of the modulus of continuity by a mixed fractional integration  

 of order 

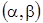
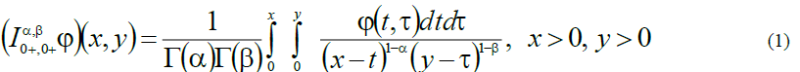
                                   where  

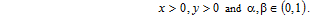
It should be emphasized that the presence of weight significantly affects the nature of the Zygmund type evaluation. This was known in the case of Zygmund type estimates for fractional integrals of functions of one variable.

This paper is devoted to the study of certain properties of the mixed fractional integral (1) in weighed generalized Hölder spaces of a function of two variables defined by mixed modulus of continuity.

We consider the operator (1) in  

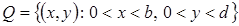
2. Preliminary information and notations

When studying the properties of continuous functions of several variables, in particular, two variables, the following classes of functions arise:

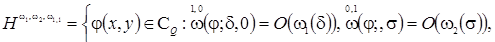
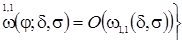
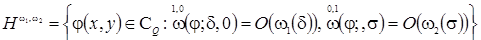
Where   

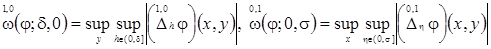
   are the partial modulus of continuity of the first order, and   

       is mixed modulus of continuity of order (1, 1); 

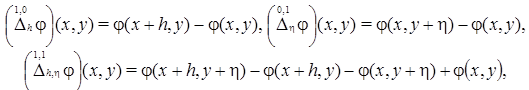
  (Definition of classes  

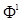
and 

see below).

 The following identity is valid

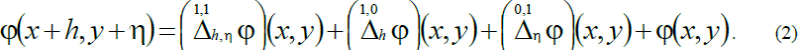
Definition 1. Let function   

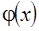
 is a bounded on  

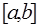
 The modulus of continuity of 

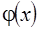
  is the expression

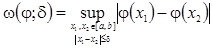
is defined for all 

 that satisfy the condition

Definition 2. A function 

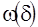
   is called a modulus of continuity if it satisfies conditions     

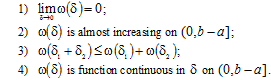
Definition 3. We denote by  

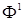
  the class of functions the class of functions 

 defined on  

 and satisfying conditions

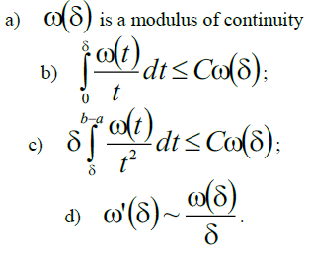
It follows from the definition 

 that this function belongs to 

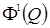
 each of the variables. In addition, we note the inequality

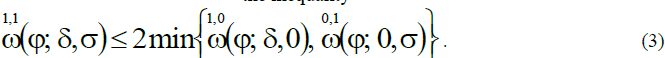
Definition 4. We denote by 

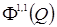
 the class of functions of two variables  

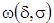
 satisfying conditions:

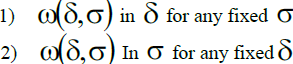
We call this class the class of mixed modulus of continuity of the first order of continuous functions of two variables.

In [1] was shown that the properties 1) and 2) are characteristic for continuity modulus in the sense that for every 

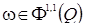
  there exist such a function 

  that

Definition 5. Let us denote  

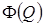
 the set of satisfying 

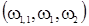
Where C – is not envy from 

Let 

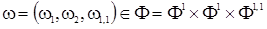
 We have introduced a norm in   

   space

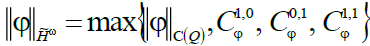
Where                     

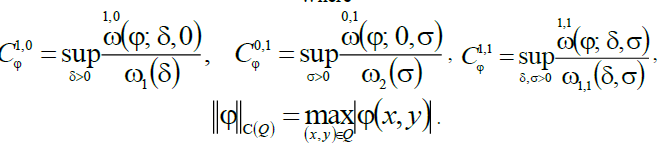
Definition 6. We say that 

   if    

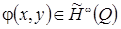
 and

We will also make use of the following weighted spaces. Let  

 be a non-negative function on  Q (we will only deal with degenerate weights 

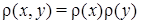
Definition 7. By  

 we denote the space of functions 

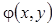
   such that 

 respectively, equipped with the norm

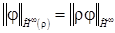
By  

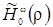
 we denote the corresponding subspaces of functions  

 such that 

Below we follow some technical estimations suggested in [3] for the case of one-dimensional Riemann - Liouville fractional integrals. We denote

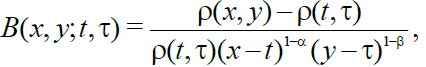
Where   

 In the case                       

 we have

                           (4)

Where

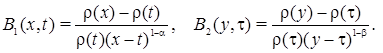
Let also

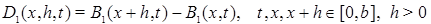
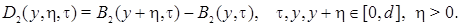
Lemma 1. ([3]) Let 

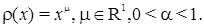
 Then

                                (5)

             (6)

Similar estimates hold for  

    and  

  with 

Remark 1. All the weighted estimations of fractional integrals in the sequel are based on inequalities (5)-(4). Note that the right - hand sides of these inequalities have the exponent 

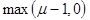
, which means that in the proof it suffices to consider only the case 

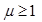
, evaluations of 

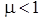
, being the same as for 

.

The following statements are known, begin first proved in (see also [17], p. 197). However, here we give a sketch of the proof of this lemma, in order to compose the representation of lightness for the two-dimensional case. Consider the one-dimensional fractional Riemann-Liouville integral

Theorem 1. Let 

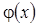
be continuous on 

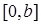
, and 

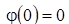
. For the fractional integral (7), the estimate

Is valid.
Proof. Representing (7) as 

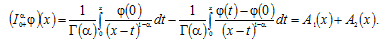
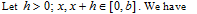
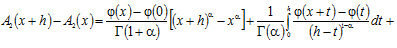
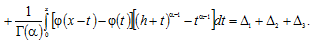
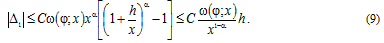
From the inequalities (24) and (25) follows the assertion of the theorem.