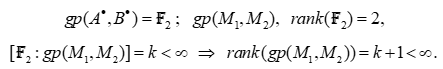AUCTORES
Globalize your Research
Research Article | DOI: https://doi.org/10.31579/2690-0440/012
Rue du Bon Pasteur, 57070 Metz, France.
*Corresponding Author: Serge Perrine, Rue du Bon Pasteur, 57070 Metz, France.
Citation: Serge Perrine. (2023). Construction of Cohn Triples and Applications. J. Mathematical Methods in Engineering, 4(1): Doi:10.31579/2690-0440.2022/012
Copyright: © 2023 Serge Perrine, this is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.
Received: 01 July 2022 | Accepted: 17 September 2022 | Published: 01 April 2023
Keywords: cohn triples; fricke relations; fibonacci numbers
Cohn triples of matrices and their links with the theory of free groups of rank were discovered in 1955 by Harvey Cohn. A lot of consequences were developed for the modular group SL (2, Z) and the free subgroup F2 In the present article, we deal with a new construction of such triples and resulting Diophantine equations.
1 Introduction
2 A new construction of the Cohn triples
3 Links with the Fibonacci numbers
4 Final result for the free group with two generators
5 Acknowledgments
6 References
We deal in the present article with the Markoff spectrum M as defined by [1]. The minimum  of an indefinite binary quadratic form of an indefinite binary quadratic form
of an indefinite binary quadratic form of an indefinite binary quadratic form

with real coefficients and positive discriminant  is
is
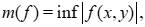
where the infimum is taken over all the pairs of integers  not both zero. The set of values not both zero. The set of values
not both zero. The set of values not both zero. The set of values  is defined as being the Markoff spectrum M.
is defined as being the Markoff spectrum M.
With the reduction of the form  to
to  we have the possibility of computing the values
we have the possibility of computing the values  with doubly infinite sequences
with doubly infinite sequences 
We have

We go from  and from
and from  with
with  matrix with integer coefficients. Its determinant is often 1, but it will be possible to find another value -1 for the determinant of our matrices, and corresponding to a matrix of
matrix with integer coefficients. Its determinant is often 1, but it will be possible to find another value -1 for the determinant of our matrices, and corresponding to a matrix of  More important, we will use the transpose of
More important, we will use the transpose of 
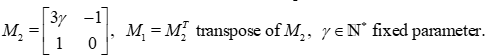
Also  (modular group) when
(modular group) when  When multiplied, these matrices yield
When multiplied, these matrices yield
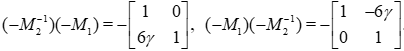
Transposing the second equality and adding it to the first one, we find a relation similar to the Heisenberg relation:
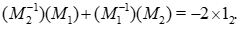
In what follows, we generalize the computations made by Cohn [6], [7], [8], in à set of articles trying to approach Markoff’s forms through modular functions:

We see that the trace of the last commutator is not a multiple of 3. So we try to generalize the result quoted in the mémoire [9], saying that
Property 1. - For two matrices  the following are equivalent:
the following are equivalent:
1/ The couple  generates the free group
generates the free group 
2/ The triple  is a solution of the Markoff equation
is a solution of the Markoff equation  .
.
3/ We have  .
.
Moreover, if  is another generating system for
is another generating system for  the free group generated by
the free group generated by  there exists one and only one
there exists one and only one  integer matrix and
integer matrix and  up to a sign, verifying the conditions
up to a sign, verifying the conditions
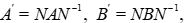
if and only if we have

Proof. See [17] (Chap. 6). Prop. 4.1 page 170 for  Prop. 4.3 page 174 for
Prop. 4.3 page 174 for  Also [9] (Chap. 6). Prop. 6.0.1 page 57 for
Also [9] (Chap. 6). Prop. 6.0.1 page 57 for  Prop. 6.0.2 page 57 for
Prop. 6.0.2 page 57 for  The equivalence
The equivalence  is a consequence of the formula of Fricke
is a consequence of the formula of Fricke  ( [17] page 160). For the remaining part: ( [17] Chap. 6. prop. 5.1 page 175). W
( [17] page 160). For the remaining part: ( [17] Chap. 6. prop. 5.1 page 175). W
2.1 Initial attempt to build a Cohn triple
We could choose, in order to have 

But this gives for C and A the same trace, which is limited enough, and a trace of B not a multiple of 3.Also:

We keep  and put
and put  , two matrices being built with
, two matrices being built with  ,the matrices to be determined. Let us write, with
,the matrices to be determined. Let us write, with  and
and  , and compute, where the interesting cases seem to be
, and compute, where the interesting cases seem to be 
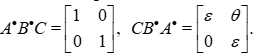
We start with
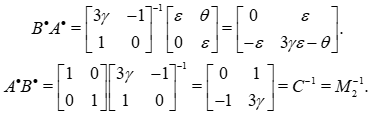
As  we have, because we suppose
we have, because we suppose  and
and 
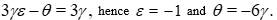
We can give new parameters defining  , and new ones defining
, and new ones defining  :
:

We write these two equations in dimension 4 and invert the matrices, after defining and verifying that
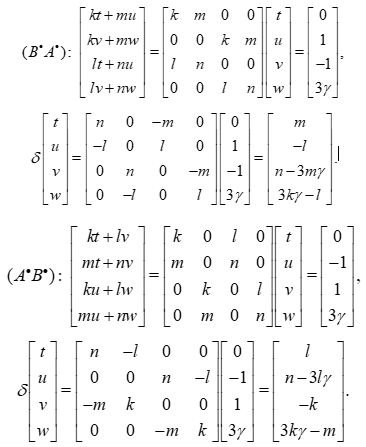
Now we solve:
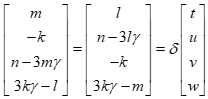
This gives  and
and  for
for  , so an expression of
, so an expression of  with two new parameters is as follows:
with two new parameters is as follows:  and
and 

For  , it is also easy to write it with the same two parameters:
, it is also easy to write it with the same two parameters:

A simpler calculation is possible, here presented in order to confirm the previous one:
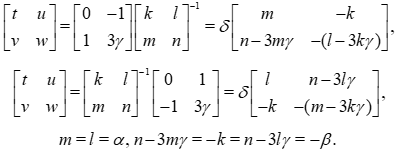
Hence, we obtain (2), (3), (5) more completely than (4), and with the expressions for  and
and  :
:

We find also some new expressions which are easy to establish:
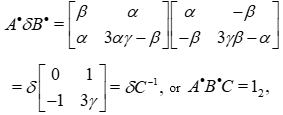
with 

then, defining K:
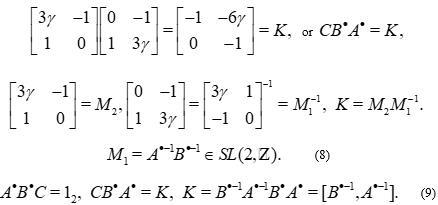
The asymmetric position of  at the front of
at the front of  , not
, not  , provokes a question. Replacing
, provokes a question. Replacing  by
by  is the answer to the question. The condition for
is the answer to the question. The condition for  and
and  to be in
to be in  does not imply the same property for
does not imply the same property for  and
and  . These matrices are in
. These matrices are in 
when their determinant  is -1, and they are in
is -1, and they are in  . We have two cases, owing to the fact that
. We have two cases, owing to the fact that  can have two values,
can have two values,  . In the two cases we exhibit a non trivial example.
. In the two cases we exhibit a non trivial example.
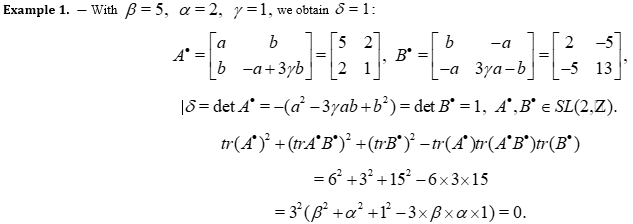
We obtain a formula linking together the matrices  and
and  , situated in
, situated in  . With
. With  , this gives the triple
, this gives the triple  introduced in ( [17] Chap. 6. page 162), associated to (5,2,1) W
introduced in ( [17] Chap. 6. page 162), associated to (5,2,1) W
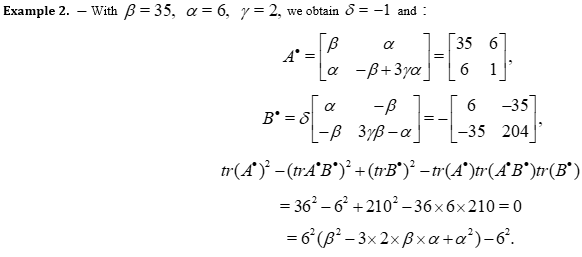
We obtain a formula linking together the matrices  , which are situated in
, which are situated in  .
.
In both cases, we can evaluate  :
:
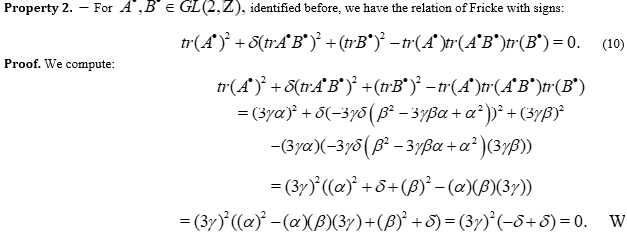
Two cases have been defined owing to the fact that  can have two values,
can have two values,  . To determine
. To determine  , we got a Diophantine equation (4) which is easy to solve.
, we got a Diophantine equation (4) which is easy to solve.
3.1 First case ( )
)
We find  , and
, and  , We deal with the Diophantine equation
, We deal with the Diophantine equation

It has been already studied in [2], and we have:
Property 3. The Diophantine equation  has solutions if and only if
has solutions if and only if  .
.
Proof. The references ([2], Theorem 6.3.1. p. 150) [21], [16]) give all that is needed about the solutions. W
Any solution  of this equation corresponds by a 1 to 1 to correspondence to
of this equation corresponds by a 1 to 1 to correspondence to  , a solution of the equation
, a solution of the equation  . We have only to look at our equation
. We have only to look at our equation  , to get all the solutions of the other. Moreover, the matrices
, to get all the solutions of the other. Moreover, the matrices  and
and  are in
are in  . It is interesting to realize that with
. It is interesting to realize that with  ,
,

Applying Fricke’s formula ([17] p. 160, Prop. 2) and simplifying
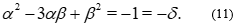
This equation is solvable in integers with a method obtained from the classical Markoff theory. The solutions are written with the Fibonacci sequence (OEIS A000045). We find in [2], [16], all the solutions: (1,1),(-1,-1) and for all  :
:

For n=1, we get

For all the couples of solutions, if  is one of them
is one of them  is another:
is another:

We find a figure with four sequences connected at the end of each other, at the singular solution (1,1). But with bisequences  , defined as indexed by Z, the Fibonacci bisequence gives
, defined as indexed by Z, the Fibonacci bisequence gives
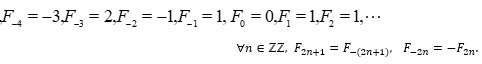
Hence we can write, on the upper infinite dihedral group  , a bisequence
, a bisequence  to name the nodes of
to name the nodes of  , but this constrains us to use the second group
, but this constrains us to use the second group  for the other bisequence
for the other bisequence  . We will give another notation in the sequel, where
. We will give another notation in the sequel, where  will be replaced by
will be replaced by  if and only n is even, and so on for the three couples obtained by permutation of
if and only n is even, and so on for the three couples obtained by permutation of  and multiplication of the two terms of the couple by -1. With this method we find a bisequence of pairs of positive Fibonacci numbers which are the positive solutions of the equation
and multiplication of the two terms of the couple by -1. With this method we find a bisequence of pairs of positive Fibonacci numbers which are the positive solutions of the equation  This corresponds to the infinite cyclic group
This corresponds to the infinite cyclic group  , in the upper position in Figure 1.
, in the upper position in Figure 1.


We see with the negative Fibonacci numbers a structure of a group isomorphic to  . We can also say that the matrix
. We can also say that the matrix  operates on the set of solutions.
operates on the set of solutions.
Remark 1. We have given in [20] the relation

Together with the same relation for 
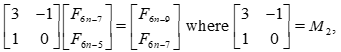
The commutative group  , operates on solutions of the equation
, operates on solutions of the equation  It is not the corresponding infinite dihedral group
It is not the corresponding infinite dihedral group  , not studied here. W
, not studied here. W
But a formula such as that one which will be true for  is more complicated, and does not seem to be given in any of the numerous articles written about Fricke’s formula. Working on this, we found:
is more complicated, and does not seem to be given in any of the numerous articles written about Fricke’s formula. Working on this, we found:

This equation has been studied in [2] (pp. 130–150), and we have:
Property 4. The Diophantine equation  has solutions if and only if
has solutions if and only if  .
.
Proof. The reference [2] gives all that is needed about the solutions.
We deal with matrices situated in  but not in
but not in  . We give the continued fraction of
. We give the continued fraction of  , the root of
, the root of  :
:
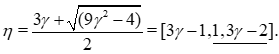
We produce then the classical table of the values of the associated form. For  we have
we have  , and we find with the following table two classes of solutions, couples of Fibonacci numbers up to signs, of the equation
, and we find with the following table two classes of solutions, couples of Fibonacci numbers up to signs, of the equation  of the first case:
of the first case:
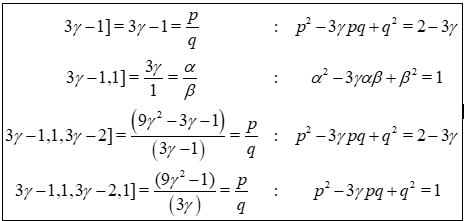
We see that the matrix  plays an important role for the transportation of the period of
plays an important role for the transportation of the period of  :
:

This gives all the solutions of the equation  , with a sign
, with a sign  corresponding to the cycle
corresponding to the cycle  and the infinite cycle
and the infinite cycle  given by
given by  :
:

In the present case,  . We would like to be able to apply some relation similar to Fricke’s formula, for example, the last expression of [17] (p. 28).
. We would like to be able to apply some relation similar to Fricke’s formula, for example, the last expression of [17] (p. 28).
But a formula such as that one which will be true for  is more complicated, and does not seem to be given in any of the numerous articles written about Fricke’s formula. Working on this, we found:
is more complicated, and does not seem to be given in any of the numerous articles written about Fricke’s formula. Working on this, we found:
Property 5. For any matrices  , we have the generalized Fricke’s formula:
, we have the generalized Fricke’s formula:

Proof. Let
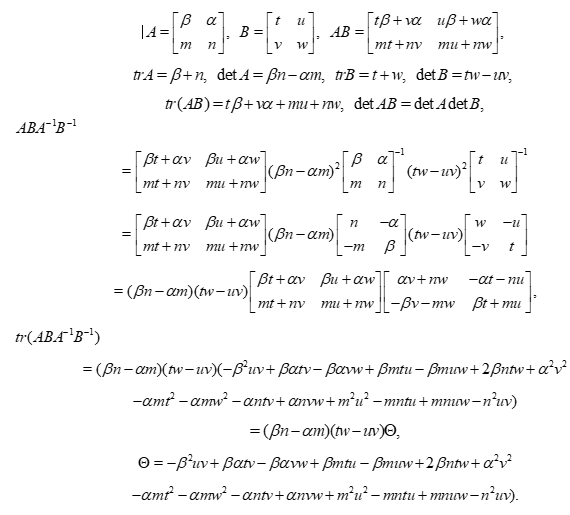
Then
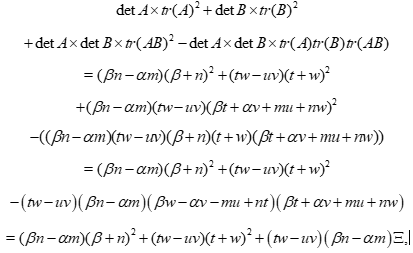
With
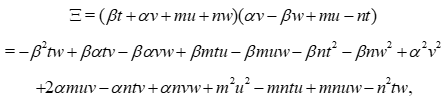
and so we find
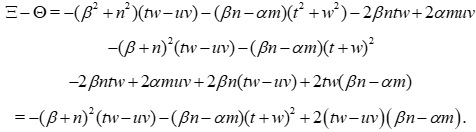
Now we combine:
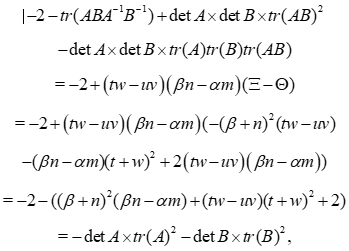
and we get
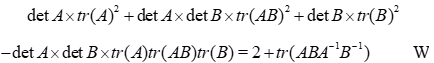
Here, the commutator to deal with is  . And we are in the parabolic case if and only if
. And we are in the parabolic case if and only if  .
.
Example 3. With  and for example
and for example 
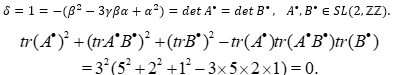
We are in the case of the positive Fricke’s relation, linking together the matrices  , situated in
, situated in  . With
. With  , the triple
, the triple  introduced in ([17] Chap. 6. page 162), is associated to (5,2,1). W
introduced in ([17] Chap. 6. page 162), is associated to (5,2,1). W
Example 4. With  and for example
and for example 
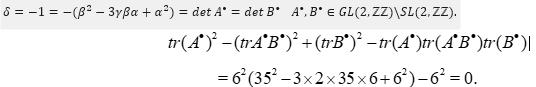
We obtain a formula linking together the matrices  , which are situated in
, which are situated in  .
.
Remark 2. The cases with which we deal in Property 2 and Property 5 are different. In the first case,  are linked with strong constraints by the common coefficients
are linked with strong constraints by the common coefficients  , and their positions inside these matrices. On the contrary, Property 5 is true for any matrices
, and their positions inside these matrices. On the contrary, Property 5 is true for any matrices  .
. 
Example 5. With  and for example
and for example

we are not in the parabolic case. Moreover, we verify Property 5:

We face the fact that the group  generated by
generated by  is free. By Property 1 and
is free. By Property 1 and  ,
,  generate the free group
generate the free group  in
in  . This group countains
. This group countains  and
and  .
.
Property 6. The subgroup  of
of  is free and isomorphic to
is free and isomorphic to  , but not equal to
, but not equal to  .
.
Proof. The group  generated by
generated by  is a subgroup of
is a subgroup of  , hence by the theorem of Nielsen–Schreier ([14] p. 92), it is a free subgroup of
, hence by the theorem of Nielsen–Schreier ([14] p. 92), it is a free subgroup of  . But
. But  confirms with Property 1 that
confirms with Property 1 that  is not a system of generators of
is not a system of generators of  .
.
A confirmation that  is a free group is not given by the properties of the commutator of
is a free group is not given by the properties of the commutator of 
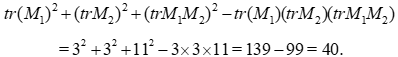
and not through Property 1, because
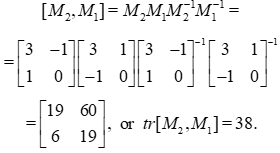
The rank, which is the number of generators of a free group, is 2 for  . The index of the subgroup
. The index of the subgroup  of
of  , denoted by
, denoted by  may be used:
may be used:
1/ Suppose k is infinite. We are in a situation where  is a free group and
is a free group and  , not a group with one element, has infinite index in
, not a group with one element, has infinite index in  . Then
. Then  is of infinite rank ([4] p. 355). But this is false, because this group has two generators
is of infinite rank ([4] p. 355). But this is false, because this group has two generators  hence a rank less than 2. This case is impossible.
hence a rank less than 2. This case is impossible.
Note that in  , the derived group,
, the derived group,
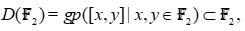
has infinite rank ([4] Théorème (9.39) p. 355 or [15] prop. 3.1. p. 13):
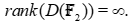
2/ Suppose k is finite. We have ([15] Proposition 3.9. p. 16):

Because our free groups  and
and  have two generators, the former relations give :
have two generators, the former relations give :
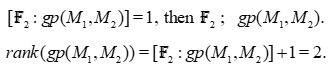
The conclusion is that  , not
, not  . It would be more comforting if
. It would be more comforting if  could be written with words in
could be written with words in  . The conclusion would be an equality. But this does not happen: only the isomorphism is sure. W
. The conclusion would be an equality. But this does not happen: only the isomorphism is sure. W
Property 1 is verified with  , not
, not  , and we have (6). If we could write
, and we have (6). If we could write  as a word of
as a word of  , we could write
, we could write  the same way, and conversely
the same way, and conversely
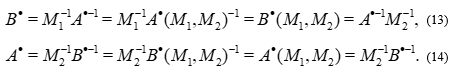
We would like to conclude that  and
and  so
so  . But this is not true, and we have only
. But this is not true, and we have only

Remark