Purpose

The topic of the presented paper concerns the mutually influences of dynamic of viscosity changes of the human sweat during the flow in thin gap between human skin and tightly fitting sport clothes (underwear) on the human metabolic age, hence on a healthy human’s lifespan.

Material And Devices

During the performed research had been applied postoperative preparations and samples of human skin. Moreover had been used inorganic sport wear equipment and following measurement devices: Segmental Body Composition Analyzer Tanita MC 780MA, AFM, pedometer Garmin Ltd.2015. The author gained experience in Germany research institutes, and practical results were obtained after measurements and information from students and patients.

Methods

The presented methods are applied in the form of performed sweat lubrication measurements of the human skin. Moreover are performed analytical and numerical calculations using Mathcad Professional Program 15 by virtue of some solutions of hydrodynamic lubrication equations and matter conversion and metabolism equations.

Results

The results presented in this paper indicated the mutually connections between human skin and underwear features with the basal metabolic rate. Moreover are indicated relations between underwear material properties and suit fashions on the human Metabolic Age (MA).

Conclusions

1.The increments of the human Basal Metabolic Rate (BMR) and more significant drops of human Metabolic Age (MA) indirectly depend on sweat dynamic viscosity increases and rise after exercises activity such as weight lifting

2.If the elastic modulus of the clothing (underwear) material increases, and it happens after training activity with material wettability changes, then: a) for lubrication by squeezing, the Basal Metabolic Rate (BMR)values increase, while the human Metabolic Age (MA) decreases; b) for rotating lubrication, The Basal Metabolic Rate (BMR) values decrease, while the human Metabolic Age (MA) decreases more slowly or increases

3.Indication of the proper kinds of skin-sweat lubrication, underwear material features and suit fashions, to obtain after activities the best rejuvenation i.e. the largest metabolic age decreases,

The main research of the presented paper concerns the mutually connections between human Basal Metabolic Rate (BMR) and Metabolic Age (MA) in one hand and human Sweat Viscosity in second hand [1-6]. Such connections are related and implemented by the influences of material features of tightly fitting clothes, underwear [4,7,8]. The current knowledge level of human Basal Metabolic Rate (BMR) and Metabolic Age (MA) is high for physiotherapy and sports medicine [7,9-16]. According to the contemporary scientific research, human BMR & MA and health depends primarily on such many known factors. Nonetheless, experimental studies revealed that the impact of the mentioned factors, accurately described through numerous formulas in scientific papers [1,2,3], does not always correspond to reality [7,8,15,16]. This encouraged the author to explain and investigate the phenomenon of impact on a healthy human’s lifespan using biotribology methods. Such methods also apply to the influence of skin hydrodynamic lubrication with sweat viscosity changes implemented by the Training Activity (TA), clothing material features on the BMR and MA. Presented paper states the continuation of previous authors achievements in domain of the human skin-sweat-underwear hydrodynamic lubrication [15,16-21]. However at first it is necessary to define some notions. Hence now we explain some main notations (indexes) occurring in presented paper.

□ The BMR[cal/day] index is defined as the difference between the total daily energy used in Kcal and the energy expenditure during the daily human activity in Kcal. Hence, the BMR index can be said to denote how many calories one’s body burns while at rest. The Department of Nutritional Sciences at the University of Connecticut estimated the following BMR values for human age groups: 20-29 years:1,360 calories; 30-49 years:1,300 calories; and 50-70 years: 1,200 calories. The Daily Caloric Need (DCN) is the BMR value multiplied by the value of dimensionless factor α from 1.2 to 1.9 depending on human activity level.

□ The Metabolic Age:MA[year] indicates how many calories one’s body burns at rest, compared to the average BMR[cal/day] for people of a certain chronological age in the general population. According to C.J. Anderson, the MA [age in years] is commonly defined as how one’s BMR compares to the average BMR for people of the same chronological age. The human MA is converted from calories to time in years after comparing one’s BMR to the average chronological age group [14]. The success after a training activity denotes decreasing human MA values. The effect is positive (negative) when the MA is lower (higher) than the subject’s actual chronological age [7,8]. The success after a training activity denotes decreasing human MA values. The effect is positive when the MA is lower than the subject’s actual chronological age (rejuvenation). The effect is negative when the MA is higher than the subject’s actual chronological age (aging, senescence).

□ Body Mass Index (BMI) depends on the Training Activity TA and next on the human Sweat Viscosity SWV[Pas]. BMI [kg/m2] is defined as the quotient where human body mass in kg is divided by the second power of the human stature in m. The following intervals of BMI are respected: BMI<18>50.0 over obesity.

□ A Training Activity Effort (TA) unit scale was applied, with the scoring range 1 ≤TA≤5. One unit represents a sportsperson’s effort while running over a 100 m distance at 2m/s. Hence, unit level 5 denotes the effort made when running over a distance of 500 m at 2m/s.

□ Wettability (We) occurs in range from 300 for hydrophilic i.e. large absorbability material, to the 750 -850 for hydrophobic i.e. small absorbability material (clothing, underwear, tights, skin).

□ Wear-ability (Wa) unit scale was applied, with the scoring range 1 ≤Wa≤100. One unit denotes the wear presented the 1mg loss of material during the time cooperation 1000 000s i.e. 10-6mg/s

2.1. Human sweat and skin in relation with inorganic sport clothing, underwear materials

The hydrodynamic lubrication of the human skin for the thin sweat layer between human skin surface and tightly fitting clothing material, characterizes with the non-monotone variations of the sweat dynamic viscosity SWV[Pas] across the boundary layer presented in Fig.1ab.

Figure 1. a) Sweat dynamic viscosity h distribution across the thin sweat boundary layer between motionless lower skin surface 1 and movable clothing upper surface 2 with sweat viscosity h assignations to the sweat flow velocity values V1, V2 in section A and B, b) sweat flow lubrication between the clothing surface and humanoid robot skin; Notations: LA- lactic acid, 3-skin, 4-epidermis layer

The clothing, or underwear surface presented in Fig.1a is loaded by the small increasing of pressure pA in section A, and loaded by the large increasing of pressure pB in section B [22]. Human sweat in the thin gap between skin and underwear(dress) consists mostly (90 per cent) of water, electrolytes, fatty acids, Lactic Acid (LA), amino acids, carbohydrate nitrogen metabolites, such as ammonia, urea, uric acid, and Urea Water Solutions (UWS) with the following density values: 1,084 kg/m3[23]. The value range of the typical human sweat’s dynamic viscosity is between 1.21 and 4.414 mPas (cP). Male sweat contains more lactic acid (LA) than female sweat [21]. Thus, laboratory measurement results demonstrate [22] that power hydrogen ion concentration pH in male sweat is lower than in female sweat. Hence, considering the abovementioned remarks, male sweat’s dynamic viscosity is higher than that of female sweat. The skin of a healthy human typically excretes (eliminates) ca. 1,200 ml of sweat daily and, additionally, 700 ml of sweat after intensive gymnastic training. For a conventional Training Activity Effort (TA) unit scale was applied, in interval 1 to 5. The values of the ESM= Eskin of the superficial layer of human skin are included in interval:0.01GPaFigure.1 ,2ab).

Figure 2.Vertical sections of skin sample contacting with the sweat flow implemented with the values of variable elasticity modulus of the skin ESM=Eskin=E; a) First (1) epidermis zone divided in the layers: A-corneous, B- granular, C- spinous, D-basis, b) three zones: first (1) epidermis, second (2) basis skin, third (3) hypodermis

The total human skin consists of following three zones: 1-epidermis, 2-basis skin,3-hypodermis. Epidermis as the first zone (1) is divided on the following layers presented in Figure.2ab.: A-corneous epidermis with old exfoliated cells, B - granular epidermis, C-spinous epidermis, D-basis epidermis. The second zone-basis skin (2) includes: nerve, blood vessel, adenoma of the sweat gland and is from 1mm to 3 mm thick. The third zone (3) i.e. 

Hypodermis includes connective tissue with young cells and fat cells Figure.2b[14,24,25].

During the performed research were used inorganic sport clothing and underwear equipment including panty-hose, single-piece, tight-fitting gymnastic overall, sport clothing presented in Figure.3abcd, produced from elastic tricot, nylon material with its specific wettability and elasticity modulus features [22].

Figure 3. Clothing of sport suit :a,b) two piece gym body and tights-pantyhose of elastic tricot, where 0.2GPa

The values of elasticity surface modulus of the superficial layer of clothing material ESM= Ed were included in interval 0.2GPa

2.2 Measurement devices and Computer program

To the lifeless materials applied during research belong following measurement devices: Segmental Body Composition Analyzer SBCA, Tanita MC 780MA with additionally implementation of SC-240, BC-418 MA, and Rank Taylor Hobson device type of Talyscan 150 implemented with Talymap Expert Computer Program, laser and mechanical sensors pedometer Garmin ltd.2023. Moreover had been applied an IKA ROTAVISC lo-vi Complete Visco-meter, an Atomic Force Microscope (AFM) and a Scanning Microscope (ACM)[21,26-29] It is possible to perform an 8-polar bio-electrical impedance analysis (BIA).A handy printout shows result values for BMI kg/m2, BMR in Kcal/day, fat %, fat mass, desirable ranges for fat %, external human body fat in percent, internal 

human body fat in a scale from 1 to 59, total body water in percent, muscle in kg and in percent, the human bone mass in kg, synovial fluid and sweat viscosity. Obtained data were next utilized in further analytical and computer calculations using Mathcad 15 Professional Software Program to obtain finally the values of human Metabolic Age MA [30].

Here are presented the various research methods, to obtain BMR [cal/day] and M A[age] index. The methods presented in this section have been now exactly divided adequately to the final results obtained in the following parts namely:3.1-theoretical Semi-Analytical-Numerical (SAN) research methods, mutually connected and implemented with 3.2 -Experimental methods (EXM), or 3.3- anamnesis methods.

3.1. SAN research methods for sweat and materials (human skin, clothing, underwear)

Now we are going to show the semi-analytical-numerical methods of solutions to present the mutually analogous connections between, human Sweat Viscosity (SWV) during the clothing material or skin lubrication in one side and kinds of material features of gym body, gym tights in second side. In SAN methods referring Sweat Fluid (SW) lubrication are taken into account analytical hydrodynamic calculations of the sweat flow between skin and clothing surfaces or overalls during the various kinds of sport training activities presented in Figure.4abcd [16].

Figure.4.The various kinds of sport activities during the hydrodynamic sweat lubrications: a,c) by rotating; b,d) by squeezing; a,b) hydrophilic clothing material, large absorbability; c,d) hydrophobic clothing materials, small absorbability.

The problem of lubrication flow for human sweat SW implemented with power hydrogen ion concentration (pH) is described by means of the conservation of momentum, continuity, energy, heat transfer, Young -Kelvin equations, related to the hydrodynamic aspects [ 12,31,32].

The deformations of elastic, hyper-elastic and bio-anisotropic biological bodies, tissues cellular structures of human skin and gym body, gym tights material surfaces are described by the equilibrium of hyper-elasticity momentum equations, physical dependencies, compatibility equations, the heat transfer equation and material property conversion equations [24].

3.2 -Experimental methods (EXM)

In the presented scientific bio-tribology and nano-sport-medicine research, the measurements of features of non-living and living materials were applied. The realization considered examinations of mentioned features had been realized using devices presented in intersection 2.2. The bio-samples of postoperative living materials in the form of pathological human skin surfaces, are gained from PhD.DSc.J. Cwanek, Poland from Rzeszów Tech. Univ [18]. Additionally the living materials and experimental methods had been gained through experience in German research institutes, and practical results were elaborated after measurements and information from students and patients after gymnastic and physical rehabilitation [26,27]. Human sweat dynamic viscosity SWV[Pas] values had been measured in laboratory form by way of the pilocarpine iontophoresis using the Gibson-Cook method [13,23,26]. Experimentally values of B M R[cal/day] and M A[year] are obtained from SBCA device [29] and next compared with the same values obtained in analytical and numerical way. The differences not exceed 5 percent.

4.1 General results

Using the material, devices and methods presented in foregoing intersections, the general results are now presented for a rotational and squeezing, periodic and unsteady, isothermal, incompressible, viscoelastic SWV flow lubrication, inside the gap height depended on unsteady time t[s]. Using the matter conversion [24] and elasto-hydrodynamic equations, we obtain in numerical way the BMR, MA values depended on the elasticity of superficial layer material modulus ESM[Pa], wettability 300 Fig.5. The SWV[Pas] for SW, denoted by ηT [Pas] and indicated in Fig.6 had been formulated in curvilinear orthogonal coordinates ai (i=1,2,3) in the following form [4,18,28]:

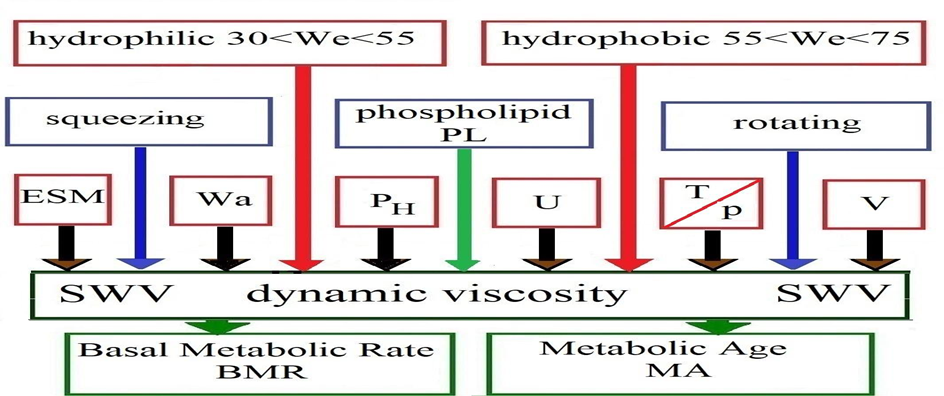
Figure 5. Human BMR,MA depended on bio-fluid dynamic viscosity (SWV), as a function of: ESM-elasticity modulus of superficial layer material, We-wettability of material (skin, clothing),Wa- wear-ability of the material, pH-power hydrogen ion concentration of the bio-fluid ( liquid, fluid, sweat),p-hydrodynamic pressure, U-the urea water solution component in considered bio-liquid, T- temperature, v- average velocity of the considered lubricated bio-liquid flow, whereas: hydrodynamic pressure p [Pa], temperature T [K],bio-liquid or sweat velocity components vi[m/s] for i = 1, 2, 3, and the joint gap height or the distance between skin and overall or underwear ε (α1, α 3) [m],k = 1.38054∙10–23[J/K]-Boltzmann constant, 1

4.2 Particular results for human sweat and skin with gym clothing cooperation

Now we are presented the particular cases of general results contained in intersection 4.1 and restricted to the human skin, sweat, gym overall, clothing cooperation with its influence on the BMR& DCN[Kcal/day] and human M A[years]. Using computer calculations implemented with measurements, in mentioned influences are considered squeezing, rotating actions with parameters ESM [Pa], We, for skin and gym overall and SWV [Pas] dynamic viscosity for the sweat. For skin and gym overall had been assumed constant values of Wear-ability Wa=50, temperature T=293K, hydrodynamic pressure p=0.0015 MPa. For sweat are taken into account constant values of urea water solutions U with density 1.07 kg/m3, constant value of hydrogen ion concentration pH=6. Moreover sweat and skin diseases are neglected. In this research are used semi-analytical SAN methods presented in intersection 3.1, the experimental EXM methods illustrated in intersection 3.2 implemented with devices indicated in intersection 2.2. Figure.6 illustrates the sweat dynamic viscosity SWV[Pas] versus elasticity surface modulus ESM[Pa] of skin Eskin and gym overall material Ed, during the squeezing and rotation lubrication for wettability variations depended on the hydrophilic and hydrophobic overall material. Presented values are obtained for following constant values: wear-ability Wa=50, temperature T=297K, shear rate of sweat flow Q=500 1/s. The changes from hydrophilic to hydrophobic materials, are connected with the ESM[Pa] increments [ 7,13]. The ESM[Pa] increments (from hydrophilic to hydrophobic) during the rotating lubrication, imply the SWV[Pas] decrements. And the ESM[Pa] increments during the squeezing lubrication lead to the SWV[Pas] increments [13]. For hydrophilic lubrication, the SWV[Pa] values obtained for rotating lubrication are larger than the SWV[Pa] values for squeezing lubrication (A>B). For hydrophobic lubrication the SWV[Pa] values obtained for squeezing lubrication are larger than the SWV[Pa] values obtained for rotating lubrication (compare Fig.6, D>C and Figure,7c)

Figure 6 Illustration of the sweat dynamic viscosity (SWV) versus elasticity surface modulus (ESM) of skin and gym clothing dress material, during the lubrication by squeezing B,D and by rotating A,C, for hydrophilic A,B( large absorbability) and hydrophobic C,D (small absorbability ) facilities of gym dress material connected with the wettability properties.

Figure 7abc illustrates the particular connections between values relations of squeezing and rotation activities for sweat dynamic viscosity values h= SWV versus the underwear elasticity surface modulus values E=ESM on the analogy of Fig.6. The new results presented in Fig.7abc are obtained for underwear presented in Fig.4abcd but now performed from nylon clothes whereas are assumed following parameters: wear-ability Wa=20, temperature T=297K, shear rate of sweat flow Q=500 1/s, power hydrogen ion concentration pH=6, urea water solution in the sweat U=1.07 kg/m3, dimensionless flow index for non-Newtonian sweat properties n = 0.95. Considered nylon material has the values E for elasticity surface modulus ESM in interval from 0.70 GPa to 1.50 GPa according to the sweat wettability intensively We. The values depicted in Fig.8abc are obtained after numerical calculations and experiment measurements. Figure.7c shows that same value E of elasticity surface modulus of underwear hydrophobic material implies larger sweat dynamic viscosity during the squeezing than in rotating lubrication. And the same values E of elasticity surface modulus of underwear hydrophilic material implies larger sweat dynamic viscosity during the rotating than in squeezing lubrication. Fig.7b shows that the values of elasticity surface modulus E decrements from underwear hydrophobic to hydrophilic material implies decrements of sweat dynamic viscosity for squeezing and sweat dynamic viscosity increments for rotating lubrication.

In Figure.8 the dependences between SWV[Pa] values and BMR&DCN[Kcal/day], M A[years] (human Metabolic Age) are now illustrated, based on previously obtained authors results [7,33], computer calculation of analytical solutions of matter conversion and metabolism equations implemented with the measurements [8]. The Sweat dynamic viscosity (SWV) presented in horizontal axis in Figure.8a depends on the material wettability (We), elasticity surface modulus of material (ESM), training activity (TA), lactic acid (LA) contained in sweat. Simultaneously the kinds of squeezing and rotating lubrication of hydrophobic and hydrophilic materials are here taken into account. The presented data depicted on the Fig.8a are obtained for constant wear- ability value Wa=50, temperature T=297K, power hydrogen ion concentration pH=5, shear rate Q=500 1/s of the sweat flow. The arrow of the first (right) vertical axis in Fig.8a shows the positive direction of the growth of BMR values in Kcal/day. The arrow of the second (left) vertical axis in Fig.8a presents the positive direction of M A[years] values decrements in years. The dynamic viscosity increments, presented by the arrow in horizontal axis, imply the growth increases of BMR[Kcal/day] values and lead to the increases of M A[years] decrements i.e. rejuvenation. The results presented in Fig.9a are respected simultaneously to the squeezing and rotating lubrication mainly for hydrophobic materials illustrated in Figure.8b.

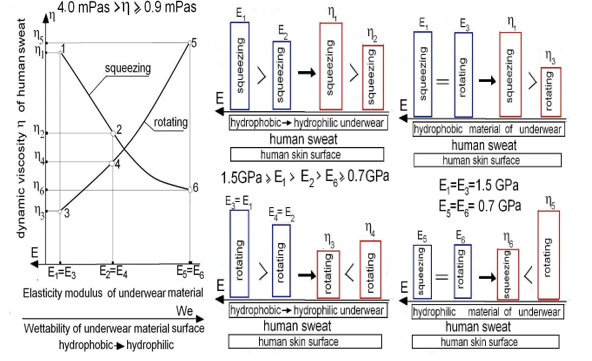
Figure.7.Sweat dynamic viscosity h versus elasticity surface modulus E of nylon underwear, implemented with particular values illustrations between the squeezing and rotating lubrication activities: a)graphical illustrations of the functions for rotating and squeezing nylon material lubrication, b)relations from hydrophobic to hydrophilic underwear material, for different values of elasticity surface modulus E and corresponding different sweat dynamic viscosity values, c) comparisons between hydrophobic and hydrophilic underwear materials, for the same values of elasticity surface modulus E and corresponding different sweat dynamic viscosity values

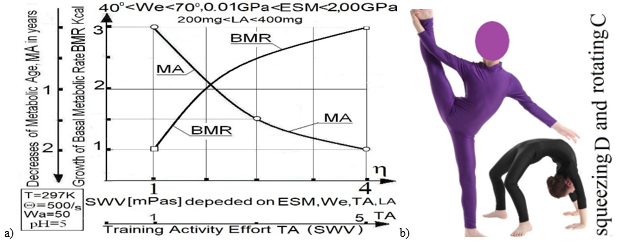
Figure 8.The metabolic values BMR and MA depended mainly on sweat viscosity, material elasticity modulus ESM[Pa] ,temperature T[K],lactic acid LA[mg], shear rate Q=500 1/s flow, power hydrogen ion concentration pH , wear ability properties Wa of the material and wettability We i.e. absorbability properties of the material: a)The BMR[Kcal/day] increments and human metabolic age MA[years] increments of decrements i.e. MA decrements versus increments of Sweat Dynamic Viscosity SWV[mPas] values, b) squeezing and rotating lubrication activities corresponding with the graphical charts, Based on previously obtained authors results [7,8] after computer calculation of analytical solutions of matter conversion and metabolism equations implemented with the measurements, the squeezing and rotating lubrication, are now illustrated in Fig.9ab. Here are presented Basal Metabolic Rate BMR DCN[Kcal/day] increments (decrements) with human Metabolic Age MA[years] decrement (increments) values, versus Elasticity Surface Modulus increment values in interval 0.1 GPa

Figure 9.The BMR[Kcal/day] and human metabolic age MA[years] variations versus Elasticity Surface Modulus ESM [GPa] increments , depended mainly on Sweat dynamic viscosity SWV[mPas] values, temperature T[K],lactic acid LA[mg], shear rate Q=500 1/sflow, power hydrogen ion concentration pH , wear ability properties Wa of the material and wettability We i.e. absorbability properties of the material, 1.2<α<1 Wa=50, T=297K, pH=5,>

The increments of the ESM[GPa] for the squeezing lubrication, presented by the arrow in horizontal axis in Fig.9a, imply the increases of the sweat viscosity SWV[Pas] and changes from hydrophilic to hydrophobic properties of the clothing (or overall) material. The mentioned increments of the ESM[Pa] presented in Fig.10a denote the training squeezing activity changes from B to D presented in Fig.6 and simultaneously denote the changes of the using of the sport clothing material from the two piece b to the one piece d presented in Fig.5 during the training activity. The increments of the Elasticity Surface Material ESM [GPa] for squeezing lubrication, presented by the arrow in horizontal axis, imply indirectly the growth increases of BMR&DCN [Kcal/day] values and lead to the increases of the decrement of the human metabolic age M A[years] i.e. rejuvenation. This phenomenon valid because ESM increments imply hydrodynamic pressure and next built human muscle mass, increasing resting energy consumption. The more muscle mass in the physician composition, the higher is BMR required to sustain their body at a certain level [7]. After computer calculations for squeezing lubrication follows, that if in sweat the values of density of urea water solution increases in interval: 1.08 [ kg/m3] Figure.9a follows, that if the shear rate of the sweat flow increases in interval: 100 [ 1/s] From obtained results presented in the right hand side of the Figure.9a follows, that the best rejuvenation (i.e. largest MA decreases) and best largest basal metabolic rate effect, had been attained after gymnastic squeezing activity realized using elastic nylon hydrophobic small absorbability one piece gym overall material presented in Fig.7 c,d with large Elasticity Surface Modulus (ESM), and during the squeezing training activity of type D.

The increments of the ESM[GPa] for the rotating lubrication, presented by the arrow in horizontal axis in Figure.9b, imply the decreases of the sweat viscosity SWV[Pas] and changes from hydrophilic to hydrophobic properties of the clothing (or overall) material. The increments of the E S M[pa] presented in Figure.9b denotes the training rotating activity changes from A to C presented in Fig.6 and simultaneously denotes the changes of the using of the two pieces a to two pieces c sport clothing,underwear material presented in Fig.4 during the training activity.

The increments of the Elasticity Surface Material ESM[GPa] for rotating lubrication, presented by the arrow in horizontal axis, imply the decrements of BMR[Kcal/day] values and lead to the decreases of the decrement (i.e. increments) of the human metabolic age M A[years]. This fact denotes the small human senescence effect, connected with the smaller decreases of MA i.e. more slowly rejuvenation.

After charts presented in Figure.9b follows, that if the shear rate of the sweat flow increases in interval: 100 [ 1/s] Figure.9b follows, that the best rejuvenation (i.e.largest MA decreases) and best largest basal metabolic rate effect, had been attained after gymnastic rotating activity realized using two piece gym suit of elastic nylon hydrophilic large absorbability material presented in Fig.7 a,b with small Elasticity Surface Modulus (ESM), and during the rotating training of type A.

□The best rejuvenation (i.e.largest MA decreases) and best largest basal metabolic rate effect, had been attained after gymnastic squeezing activity realized using elastic nylon hydrophobic, small absorbability, one piece gym clothing material with large Elasticity Surface Modulus (ESM).

□The best rejuvenation (i.e.largest MA decreases) and best largest basal metabolic rate effect, had been attained after gymnastic rotating activity realized using two piece gym suit of elastic nylon hydrophilic large absorbability clothing material with small Elasticity Surface Modulus (ESM).

□. If the elastic modulus of the clothing (underwear) material increases, and it happens after training activity with material wettability changes, then: a) for squeezing, the Basal Metabolic Rate (BMR) values increase, while the human Metabolic Age (MA) decreases; b) for rotating, the Basal Metabolic Rate (BMR) values decrease, while the human Metabolic Age (MA) decreases more slowly or increases

□By virtue of the measurements and computer calculations we show that Dynamic viscosity (Pas) of non-Newtonian pseudoplastic human sweat increases vs:

1.Increments of pressure [N/m2=Pa],

2.Decrements of temperature from 316 K to 308K (430 C, 350 C),

3.Decrements of Shear Rate from 1000 000 Hz to 10Hz,

4.Decrements of the elasticity modulus during the rotating or linear motion of the superficial layer of skin or underwear (dress) surface which is by bio-liquid lubricated from 1000 MPa to 2MPa,

5.Increments of the elasticity modulus during the squeezing motion of the superficial layer of skin or underwear (dress) surface which is by bio-liquid lubricated from 2 MPa to 1000 MPa,

This study was funded by the WSG Bydgoszcz University, with its head office on ul. Garbary 2, Bydgoszcz, Poland. The Authors would like to thank all the persons involved in the discussions at the study preparation stage.

In previous papers [7,8,12,33,34] the authors have proven that human sweat dynamic viscosity increments during skin-sweat-clothing hydrodynamic squeezing lubrication, contribute to the increasing BMR&DCN and decreasing MA values. Additionally in this paper the author has proven that human sweat dynamic viscosity decrements during skin-sweat-clothing hydrodynamic rotating lubrication lead to the decreasing BMR and increasing MA values.

Why is this phenomenon valid? To explain this question, we show the following interpretation.

In this and in previous papers the authors show that the sweat dynamic viscosity depends and increases on many factors for example such as: sport training activity TA particularly exercises of weight lifting, increments of the elasticity modulus of material during the squeezing motion, increments from 2 to 4 of power hydrogen ion concentration, and after Mifflin-St.Jeor such factor as body mass, human stature, human age.

It is evident that dynamic viscosity increments (decrements), imply a hydrodynamic pressure increments (decrements) during human skin dynamic lubrication with sweat. Hence, this phenomenon after many exercises such as weight-lifting indirectly lead to higher BMR because they build muscle mass increasing resting energy consumption. The more muscle mass, the higher the BMR. Moreover by virtue of experimental measurements and of analytical considerations of energy conversion and conservation follows, that the total energy and fat increase calorie burning by enhancing the breakdown of fat cells. The additionally obtained energy is converted into calories, systematically improving BMR values. Up today, to calculate the BMR value, we can use the following formulae well-known in literature, e.g., Harris-Benedict, Mifflin-St.Jeor, Katch-McArdleor the Cunningham Equation calculator [14,29]. Unfortunately, we seldom obtain the same BMR value using the formulae, where only body mass, human stature, human age influences were taking into account. According to the authors’ suggestion, the differences between Mifflin-S.Jeor result and BMR,MA values obtained in this paper follow from the fact that the referenced formulae do not consider skin lubrication influences of TA,ESM,pH on the sweat dynamic viscosity values increases and its synergistic effects and next final on the BME&DCN values.

After the authors’ knowledge, to the best achievement obtained in this paper, is the indication of proper kind of human skin and to present the proper kind of absorbability and fashion of clothing underwear or sport underwear material during the training activity to obtain the best BMR and best human rejuvenation (i.e. Largest MA decreases).

Nomenclature

AFM-Atomic Force Microscope,

BMI- Body Mass Index, kg/m2,

BMR-Basal Metabolic Rate, Kcal/day

DCN-Daily Caloric Need, Kcal/day =BMR×α,

ESM- Elasticity Surface Modulus, Pa,GPa,

EXM-Experimental Method,

Eskin –elasticity modulus of human skin,Pa

Ed –elasticity modulus of clothing (underwear) material,Pa

LA-Lactic Acid, mg,

MA-Metabolic Age, year

PL-Phospholipid

SAN-Semi Analytical Numerical method

SK-human skin,

SW-human sweat,

SWV-sweat dynamic viscosity, Pas

TA-Training Activity,

T-Temperature, K,

U-urea water solution, kg/m3

Wa-wear ability of the material, mg/s

We-Wettability, grad,

k-Bolzmann constant,J/K,

n-dimensionless flow index,

p-pressure, Pa

PH –dimensionless power hydrogen ion concentration,

v-velocity,m/s,

α-dimensionless coefficient from 1.2 to 1.9 depending on TA activity,

.h-dynamic viscosity,Pas

Q -shear rate,1/s